Numpy в python. часть 1

Добро пожаловать в NumPy!

NumPy (NumericalPython) — это библиотека Python с открытым исходным кодом, которая используется практически во всех областях науки и техники. Это универсальный стандарт для работы с числовыми данными в Python, и он лежит в основе научных экосистем Python и PyData. В число пользователей NumPy входят все — от начинающих программистов до опытных исследователей, занимающихся самыми современными научными и промышленными исследованиями и разработками. API-интерфейс NumPy широко используется в пакетах Pandas, SciPy, Matplotlib, scikit-learn, scikit-image и в большинстве других научных и научных пакетов Python.

Библиотека NumPy содержит многомерный массив и матричные структуры данных (дополнительную информацию об этом вы найдете в следующих разделах). Он предоставляет ndarray, однородный объект n-мерного массива, с методами для эффективной работы с ним. NumPy может использоваться для выполнения самых разнообразных математических операций над массивами. Он добавляет мощные структуры данных в Python, которые гарантируют эффективные вычисления с массивами и матрицами, и предоставляет огромную библиотеку математических функций высокого уровня, которые работают с этими массивами и матрицами.

Узнайте больше о NumPy здесь!

GIF черезgiphy

Установка NumPy

Чтобы установить NumPy, я настоятельно рекомендую использовать научный дистрибутив Python. Если вам нужны полные инструкции по установке NumPy в вашей операционной системе, вы можетенайти все детали здесь,

Если у вас уже есть Python, вы можете установить NumPy с помощью

conda install numpy

или

pip install numpy

Если у вас еще нет Python, вы можете рассмотреть возможность использованияанаконда, Это самый простой способ начать. Преимущество этого дистрибутива в том, что вам не нужно слишком беспокоиться об отдельной установке NumPy или каких-либо основных пакетов, которые вы будете использовать для анализа данных, таких как pandas, Scikit-Learn и т. Д.

Если вам нужна более подробная информация об установке, вы можете найти всю информацию об установке наscipy.org,

фотоАдриеннотPexels

Если у вас возникли проблемы с установкой Anaconda, вы можете ознакомиться с этой статьей:

Как импортировать NumPy

Каждый раз, когда вы хотите использовать пакет или библиотеку в своем коде, вам сначала нужно сделать его доступным.

Чтобы начать использовать NumPy и все функции, доступные в NumPy, вам необходимо импортировать его. Это можно легко сделать с помощью этого оператора импорта:

import numpy as np

(Мы сокращаем «numpy» до «np», чтобы сэкономить время и сохранить стандартизированный код, чтобы любой, кто работает с вашим кодом, мог легко его понять и запустить.)

В чем разница между списком Python и массивом NumPy?

NumPy предоставляет вам огромный выбор быстрых и эффективных числовых опций. Хотя список Python может содержать разные типы данных в одном списке, все элементы в массиве NumPy должны быть однородными. Математические операции, которые должны выполняться над массивами, были бы невозможны, если бы они не были однородными.

Зачем использовать NumPy?

фотоPixabayотPexels

Массивы NumPy быстрее и компактнее, чем списки Python. Массив потребляет меньше памяти и намного удобнее в использовании. NumPy использует гораздо меньше памяти для хранения данных и предоставляет механизм задания типов данных, который позволяет оптимизировать код еще дальше.

Что такое массив?

Массив является центральной структурой данных библиотеки NumPy. Это таблица значений, которая содержит информацию о необработанных данных, о том, как найти элемент и как интерпретировать элемент. Он имеет сетку элементов, которые можно проиндексировать в Все элементы имеют одинаковый тип, называемыймассив dtype(тип данных).

Массив может быть проиндексирован набором неотрицательных целых чисел, логическими значениями, другим массивом или целыми числами.рангмассива это количество измерений.формамассива — это кортеж целых чисел, дающий размер массива по каждому измерению.

Одним из способов инициализации массивов NumPy является использование вложенных списков Python.

a = np.array(, , ])

Мы можем получить доступ к элементам в массиве, используя квадратные скобки. Когда вы получаете доступ к элементам, помните, чтоиндексирование в NumPy начинается с 0, Это означает, что если вы хотите получить доступ к первому элементу в вашем массиве, вы получите доступ к элементу «0».

print(a)

Выход:

NumPy¶

There is now a journal article available for citing usage of NumPy:

Charles R. Harris, K. Jarrod Millman, Stéfan J. van der Walt, Ralf
Gommers, Pauli Virtanen, David Cournapeau, Eric Wieser, Julian Taylor,
Sebastian Berg, Nathaniel J. Smith, Robert Kern, Matti Picus, Stephan
Hoyer, Marten H. van Kerkwijk, Matthew Brett, Allan Haldane, Jaime
Fernández del Río, Mark Wiebe, Pearu Peterson, Pierre Gérard-Marchant,
Kevin Sheppard, Tyler Reddy, Warren Weckesser, Hameer Abbasi,
Christoph Gohlke & Travis E. Oliphant.
Array programming with NumPy, Nature, 585, 357–362 (2020),
DOI:10.1038/s41586-020-2649-2 (publisher link)

Here’s an example of a BibTeX entry:

История

В 1990-х годах Python был расширен за счет включения в него типа массива для числовых вычислений под названием Numeric (этот пакет в конечном итоге был заменен Трэвисом Олифантом, который написал NumPy в 2006 году как смесь Numeric и Numarray, которая была начата в 2001 году). По состоянию на 2000 год росло число модулей расширения и возрастал интерес к созданию полноценной среды для научных и технических вычислений. В 2001 году Трэвис Олифант, Эрик Джонс и Пиару Петерсон объединили написанный ими код и назвали получившийся пакет SciPy. Вновь созданный пакет предоставляет стандартный набор общих числовых операций поверх структуры данных числового массива. Вскоре после этого Фернандо Перес выпустил IPython , расширенную интерактивную оболочку, широко используемую в сообществе технических вычислений, а Джон Хантер выпустил первую версию Matplotlib , библиотеки 2D-графиков для технических вычислений. С тех пор среда SciPy продолжала расти с появлением большего количества пакетов и инструментов для технических вычислений .

1.6.1. File input/output: scipy.io¶

Matlab files: Loading and saving:

>>> from scipy import io as spio
>>> a = np.ones((3, 3))
>>> spio.savemat('file.mat', {'a' a}) # savemat expects a dictionary
>>> data = spio.loadmat('file.mat')
>>> data'a'
array(,
       ,
       ])

Warning

Python / Matlab mismatches, eg matlab does not represent 1D arrays

>>> a = np.ones(3)
>>> a
array()
>>> spio.savemat('file.mat', {'a' a})
>>> spio.loadmat('file.mat')])

Notice the difference?

Image files: Reading images:

>>> import imageio
>>> imageio.imread('fname.png')    
Array(...)
>>> # Matplotlib also has a similar function
>>> import matplotlib.pyplot as plt
>>> plt.imread('fname.png')    
array(...)

Проверка на нормальность в Scipy

Нормальный закон распределения является простым и удобным для дальнейшего исследования. Чтобы проверить имеет ли тот или иной атрибут нормальное распределение, можно воспользоваться двумя критериями Python-библиотеки с модулем . Модуль   поддерживает большой диапазон статистических функций, полный перечень которых представлен в официальной документации.

В основе проверки на “нормальность” лежит проверка гипотез. Нулевая гипотеза – данные распределены нормально, альтернативная гипотеза – данные не имеют нормального распределения.

Проведем первый критерий Шапиро-Уилк [], возвращающий значение вычисленной статистики и p-значение. В качестве критического значения в большинстве случаев берется 0.05. При p-значении меньше 0.05 мы вынуждены отклонить нулевую гипотезу.

Проверим распределение атрибута Rings, количество колец:

import scipy

stat, p = scipy.stats.shapiro(data) # тест Шапиро-Уилк
print('Statistics=%.3f, p-value=%.3f' % (stat, p))

alpha = 0.05
if p > alpha:
    print('Принять гипотезу о нормальности')
else:
    print('Отклонить гипотезу о нормальности')

В результате мы получили низкое p-значение и, следовательно, отклоняем нулевую гипотезу:

Statistics=0.931, p-value=0.000
Отклонить гипотезу о нормальности

Второй тест по критерию согласия Пирсона [], который тоже возвращает соответствующее значение статистики и p-значение:

stat, p = scipy.stats.normaltest(data) # Критерий согласия Пирсона
print('Statistics=%.3f, p-value=%.3f' % (stat, p))

alpha = 0.05
if p > alpha:
    print('Принять гипотезу о нормальности')
else:
    print('Отклонить гипотезу о нормальности')

Этот критерий также отвергает нулевую гипотезу о нормальности распределения колец у моллюсков, так как p-значение меньше 0.05:

Statistics=242.159, p-value=0.000
Отклонить гипотезу о нормальности

Mass:

Return the specified unit in kg (e.g.
returns )

Example

from scipy import constants

print(constants.gram)        #0.001print(constants.metric_ton)  #1000.0
print(constants.grain)       #6.479891e-05
print(constants.lb)          #0.45359236999999997
print(constants.pound)       #0.45359236999999997
print(constants.oz)          #0.028349523124999998
print(constants.ounce)       #0.028349523124999998
print(constants.stone)       #6.3502931799999995
print(constants.long_ton)    #1016.0469088
print(constants.short_ton)   #907.1847399999999
print(constants.troy_ounce)  #0.031103476799999998
print(constants.troy_pound)  #0.37324172159999996
print(constants.carat)       #0.0002
print(constants.atomic_mass) #1.66053904e-27print(constants.m_u)         #1.66053904e-27
print(constants.u)           #1.66053904e-27

Discrete Fourier Transform – scipy.fftpack

• DFT is a mathematical technique which is used in converting spatial data into frequency data.
• FFT (Fast Fourier Transformation) is an algorithm for computing DFT
• FFT is applied to a multidimensional array.
• Frequency defines the number of signal or wavelength in particular time period.

Example: Take a wave and show using Matplotlib library. we take simple periodic function example of sin(20 × 2πt)

%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np 

#Frequency in terms of Hertz
fre  = 5 
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre  * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()

Output:

You can see this. Frequency is 5 Hz and its signal repeats in 1/5 seconds – it’s call as a particular time period.

Now let us use this sinusoid wave with the help of DFT application.

from scipy import fftpack

A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()

axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()

Output:

• You can clearly see that output is a one-dimensional array.
• Input containing complex values are zero except two points.
• In DFT example we visualize the magnitude of the signal.

Что такое Python?

По состоянию на 2020 год Python является одним из самых популярных языков программирования, который входит в ТОП-10, а также считается одним из наиболее простых для обучения программированию. Если вы только начинаете изучать основы программирования, то Python для вас — лучший выбор.

На нашем сайте вы сможете пройти полный курс по языку программирования Python (читается как Пайтон или Питон) онлайн абсолютно . Курс будет полезен как для начинающих веб-разработчиков, так и для профессионалов как справочное пособие для дальнейшей работы.

Python произносится как Пайтон, но в русскоязычной среде часто произносят как «Питон», что в общем-то не является большой ошибкой. Каждый может произносить название Python как хочет или как ему удобно.

Python используется для:

• веб-разработка (на стороне сервера);
• разработка программного обеспечения;
• математика;
• системные скрипты.

Что может делать Python?

• Python может использоваться на сервере для создания веб-приложений.
• Python может использоваться вместе с программным обеспечением для создания рабочих процессов.
• Python может подключаться к системам баз данных. Он также может читать и изменять файлы.
• Python может использоваться для обработки больших данных и выполнения сложной математики.
• Python можно использовать для быстрого прототипирования или для разработки программного обеспечения, готового к производству.

Почему надо изучать Python?

• Python работает на разных платформах (Windows, Mac, Linux, Raspberry Pi и т.д.).
• Python имеет простой синтаксис, похожий на обычный английский язык.
• Python имеет синтаксис, который позволяет разработчикам писать программы с меньшим количеством строк, чем некоторые другие языки программирования.
• Python работает в системе интерпретатора, что означает, что код может быть выполнен, как только он написан. Это означает, что прототипирование может быть очень быстрым.
• Python может рассматриваться как процедурный, объектно-ориентированный или функциональный.

Что нужно знать про Python?

• Самая последняя основная версия Python — это Python 3, который мы будем использовать в этом учебнике. Тем не менее, Python 2, хотя и не обновляется ничем, кроме обновлений безопасности, все ещё довольно популярен.

• Python был разработан для удобства чтения и имеет некоторые сходства с английским языком с влиянием математики.
• Python использует новые строки для завершения команды, в отличие от других языков программирования, которые часто используют точки с запятой или круглые скобки.
• Python использует отступы, используя пробелы для определения области видимости, такие как область действия циклов, функций и классов. Другие языки программирования часто используют фигурные скобки для этой цели.

Fourier Transforms with Python SciPy

Fourier Transforms enable us to understand and depict functions as a summation of periodic components.

The sub-module of the SciPy library is used to perform Fourier transforms on the equations.

Example:

from scipy.fftpack import fft
import numpy as np

# Count of sample points
n = 400

# sample spacing
T = 1.0 / 500.0
x_i = np.linspace(0.0, n*T, n)
y_i = np.tan(70.0 * 2.0*np.pi*x_i) + 0.5*np.tan(70.0 * 2.0*np.pi*x_i)
y_f = fft(y_i)
x_f = np.linspace(0.0, 1.0/(3.0*T), n//2)

# matplotlib for plotting purposes
import matplotlib.pyplot as plt
plt.plot(x_f, 2.0/n * np.abs(y_f[0:n//2]))
plt.show()

In the above snippet of code, we have used numpy.linspace() function to get evenly spaced integers. Further, function is used to calculate the Fourier value of the input. We have used the Python matplotlib module to plot the Tangent graph.

Output:

Fourier Transforms – Tangent graph

SciPy Ndimage

The SciPy provides the ndimage (n-dimensional image) package, that contains the number of general image processing and analysis functions. Some of the most common tasks in image processing are as follows:

• Basic manipulations − Cropping, flipping, rotating, etc.
• Image filtering − Denoising, sharpening, etc.
• Image segmentation − Labeling pixels corresponding to different objects
• Classification
• Feature extraction
• Registration

Here are some examples in which we will apply some of these image processing techniques on the images:

First, let us import an image that is already included in the SciPy package:

import scipy.misc
import matplotlib.pyplot as plt
face = scipy.misc.face()#returns an image of raccoon
#display image using matplotlib
plt.imshow(face)
plt.show()

Output:

Crop image

import scipy.misc
import matplotlib.pyplot as plt
face = scipy.misc.face()#returns an image of raccoon
lx,ly,channels= face.shape
# Cropping
crop_face = face[int(lx/4):int(-lx/4), int(ly/4):int(-ly/4)]
plt.imshow(crop_face)
plt.show()

Output:

Rotate Image

from scipy import misc,ndimage
import matplotlib.pyplot as plt
face = misc.face()
rotate_face = ndimage.rotate(face, 180)
plt.imshow(rotate_face)
plt.show()

Output:

Blurring or Smoothing  Images

Here we will blur the original images using the Gaussian filter and see how to control the level of smoothness using the sigma parameter.

from scipy import ndimage,misc
import matplotlib.pyplot as plt

face = scipy.misc.face(gray=True)
blurred_face = ndimage.gaussian_filter(face, sigma=3)
very_blurred = ndimage.gaussian_filter(face, sigma=5)

plt.figure(figsize=(9, 3))
plt.subplot(131)
plt.imshow(face, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(132)
plt.imshow(very_blurred, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(133)
plt.imshow(blurred_face, cmap=plt.cm.gray)
plt.axis('off')


plt.subplots_adjust(wspace=0, hspace=0., top=0.99, bottom=0.01,
                    left=0.01, right=0.99)

plt.show()

Output:

The first image is the original image followed by the blurred images with different sigma values.

Sharpening images

Here we will blur the image using the Gaussian method mentioned above and then sharpen the image by adding intensity to each pixel of the blurred image.

import scipy
from scipy import ndimage
import matplotlib.pyplot as plt

f = scipy.misc.face(gray=True).astype(float)
blurred_f = ndimage.gaussian_filter(f, 3)

filter_blurred_f = ndimage.gaussian_filter(blurred_f, 1)

alpha = 30
sharpened = blurred_f + alpha * (blurred_f - filter_blurred_f)

plt.figure(figsize=(12, 4))

plt.subplot(131)
plt.imshow(f, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(132)
plt.imshow(blurred_f, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(133)
plt.imshow(sharpened, cmap=plt.cm.gray)
plt.axis('off')

plt.tight_layout()
plt.show()

Output:

Edge detection

Edge detection includes a variety of mathematical methods that aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities. The points at which image brightness changes sharply are typically organized into a set of curved line segments termed edges.

Here is an example where we make a square figure and then find its edges:

mport numpy as np
from scipy import ndimage
import matplotlib.pyplot as plt

im = np.zeros((256, 256))
im = 1

im = ndimage.rotate(im, 15, mode='constant')
im = ndimage.gaussian_filter(im, 8)

sx = ndimage.sobel(im, axis=0, mode='constant')
sy = ndimage.sobel(im, axis=1, mode='constant')
sob = np.hypot(sx, sy)

plt.figure(figsize=(9,5))
plt.subplot(141)
plt.imshow(im)
plt.axis('off')
plt.title('square', fontsize=20)
plt.subplot(142)
plt.imshow(sob)
plt.axis('off')
plt.title('Sobel filter', fontsize=20)
plt.show()

Output:

Optimization and Fit in SciPy – scipy.optimize

• Optimization provides a useful algorithm for minimization of curve fitting, multidimensional or scalar and root fitting.
• Let’s take an example of a Scalar Function, to find minimum scalar function.

%matplotlib inline
import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np

def function(a):
       return   a*2 + 20 * np.sin(a)
plt.plot(a, function(a))
plt.show()
#use BFGS algorithm for optimization
optimize.fmin_bfgs(function, 0) 

Output:

Optimization terminated successfully.

Current function value: -23.241676

Iterations: 4

Function evaluations: 18

Gradient evaluations: 6

array()

• In this example, optimization is done with the help of the gradient descent algorithm from the initial point
• But the possible issue is local minima instead of global minima. If we don’t find a neighbor of global minima, then we need to apply global optimization and find global minima function used as basinhopping() which combines local optimizer.

optimize.basinhopping(function, 0)

Output:

fun: -23.241676238045315
 lowest_optimization_result:
      fun: -23.241676238045315
 hess_inv: array(`0`.`05023331`)
      jac: array()
  message: 'Optimization terminated successfully.'
     nfev: 15
      nit: 3
     njev: 5
   status: 0
  success: True
        x: array()
                    message: 
      minimization_failures: 0
                       nfev: 1530
                        nit: 100
                       njev: 510
               x: array()

SciPy Interpolation

Interpolation is the process of estimating unknown values that fall between known values.SciPy provides us with a sub-package scipy.interpolation which makes this task easy for us. Using this package, we can perform 1-D or univariate interpolation and Multivariate interpolation. Multivariate interpolation (spatial interpolation ) is a kind interpolation on functions that consist of more than one variables. 

Here is an example of 1-D interpolation where there is only variable i.e. ‘x’:

First, we will define some points and plot them

import numpy as np  
from scipy import interpolate  
import matplotlib.pyplot as plt  
x = np.linspace(0, 5, 10)  
y = np.cos(x**2/3+4) 
plt.scatter(x,y,c='r')  
plt.show()  

Output:

scipy.interpolation provides interp1d class which is a useful method to create a function based on fixed data points. We will create two such functions that use different techniques of interpolation. The difference will be clear to you when you see the plotted graph of both of these functions.

from scipy.interpolate import interp1d  
import matplotlib.pyplot as plt  
fun1 = interp1d(x, y,kind = 'linear')  
fun2 = interp1d(x, y, kind = 'cubic')  
#we define a new set of input
xnew = np.linspace(0, 4,30)  
plt.plot(x, y, 'o', xnew, fun1(xnew), '-', xnew, fun2(xnew), '--')  
plt.legend(, loc = 'best')  
plt.show()

Output:

In the above program, we have created two functions fun1 and fun2. The variable x contains the sample points, and variable y contains the corresponding values. The third variable kind represents the types of interpolation techniques. There are various methods of interpolation. These methods are the following:

• Linear
• Nearest
• Zero
• S-linear
• Quadratic
• Cubic

Now what happens when we change the input values

from scipy.interpolate import interp1d  
import matplotlib.pyplot as plt  
fun1 = interp1d(x, y,kind = 'linear')  
fun2 = interp1d(x, y, kind = 'cubic')  
xnew = np.linspace(3, 5,30)  
plt.plot(x, y, 'o', xnew, fun1(xnew), '-', xnew, fun2(xnew), '--')  
plt.legend(, loc = 'best')  
plt.show()  

Output:

Датасет и Pandas для статистического анализа

В качестве анализа возьмем датасет c моллюсками вида abalone, доступный на сайте Kaggle – онлайн-площадке соревнований по машинному обучению. Датасет содержит физические параметры моллюсков: рост, диаметр, высоту, вес раковины и т.д. Также присутствует один категориальный признак – пол моллюска. Ключевым атрибутам является количество колец у моллюска, определяющего его возраст.
Для чтения данных будем использовать pandas. C основами работы pandas вы можете ознакомиться тут.

import pandas as pd
data = pd.read_csv('abalone.csv')
data.head()

Первые строчки выглядят следующим образом:

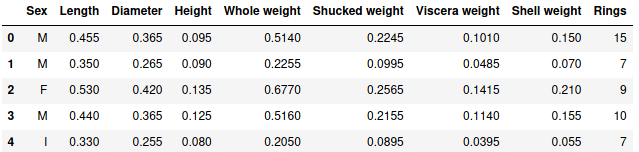
Первые пять строчек DataFrame

Volume:

Return the specified unit in cubic meters (e.g.
returns )

Example

from scipy import constants

print(constants.liter)            #0.001
print(constants.litre)            #0.001
print(constants.gallon)           #0.0037854117839999997
print(constants.gallon_US)        #0.0037854117839999997
print(constants.gallon_imp)       #0.00454609
print(constants.fluid_ounce)      #2.9573529562499998e-05
print(constants.fluid_ounce_US)   #2.9573529562499998e-05
print(constants.fluid_ounce_imp)  #2.84130625e-05
print(constants.barrel)           #0.15898729492799998
print(constants.bbl)              #0.15898729492799998

Sub-Packages in Python SciPy

There are various sub-modules available in the SciPy library to perform and enhance the efficiency of the scientific calculations.

Some of the popular sub-modules of the SciPy library are listed below:

• special: This sub-module contains the Special functions to perform a specific task.
• constants: Represents constants.
• optimize: This sub-module contains algorithms for optimization.
• integrate: This sub-module contains functions to perform Mathematical Integration.
• interpolate: Represents functions to perform interpolation.
• linalg: Represents functions to perform operations on linear algebra equations.
• io: It contains functions to perform Input/Output operations on the given input.
• fftpack: Represents functions to perform Discrete Fourier Transform.
• signal: Represents functions and tools for Signal Processing in Python.
• sparse: Represents algorithms to deal with sparse matrices.
• cluster: Represents functions to perform hierarchical clustering.

Работа с polynomial

В SciPy есть два способа работы с polynomial. Первый использует класс poly1d. Этот класс принимает коэффициенты или корни для инициализации и формирует полиномиальный объект. Когда мы печатаем этот объект, мы видим, что он напечатан, как polynomial. Давайте посмотрим на пример кода:

from numpy import poly1d

# We'll use some functions from numpy remember!!
# Creating a simple polynomial object using coefficients
somePolynomial = poly1d()

# Printing the result
# Notice how easy it is to read the polynomial this way
print(somePolynomial)

# Let's perform some manipulations
print("\nSquaring the polynomial: \n")
print(somePolynomial* somePolynomial)

#How about integration, we just have to call a function
# We just have to pass a constant say 3
print("\nIntegrating the polynomial: \n")
print(somePolynomial.integ(k=3))

#We can also find derivatives in similar way
print("\nFinding derivative of the polynomial: \n")
print(somePolynomial.deriv())

# We can also solve the polynomial for some value, 
# let's try to solve it for 2
print("\nSolving the polynomial for 2: \n")
print(somePolynomial(2))

Другой способ работы с polynomial – использовать массив коэффициентов. Существуют функции, доступные для выполнения операций с polynomial, представленными в виде последовательностей, первый метод выглядит намного проще в использовании и дает вывод в удобочитаемой форме, поэтому я предпочитаю первый для примера.

SciPy IO (Input & Output)

The functions provided by the scipy.io package enables us to work around with different formats of files such as:

• Matlab
• IDL
• Matrix Market
• Wave
• Arff
• Netcdf, etc.

The functions such as loadmat(), savemat() and whosmat() can load a MATLAB file, save a MATLAB file and list variables in a MATLAB file respectively. Here is an example:

First, save a MatLab file as test.mat which contains a structure as shown below:

Now we can use loadmat()  function to import this file into a python script as shown below:

from scipy.io import loadmat
x = loadmat('test.mat')
#save the individual elements as python object
lon = x
lat = x
# one-liner to read a single variable
lon = loadmat('test.mat')