How to install numpy

Функции перемешивания элементов массива

Следующие две
функции:

np.random.shuffle() и np.random.permutation()

перемешивают
случайным образом элементы массива. Например, дан массив:

a = np.arange(10) # array()

И нам требуется
перетасовать его элементы. В самом простом случае, это делается так:

np.random.shuffle(a) # array()

Причем, здесь
меняется сам массив a. Если вызвать эту функцию еще раз:

np.random.shuffle(a) # array()

то значения еще
раз перетасуются. Но, работает она только с первой осью axis0. Например,
если взять двумерный массив:

a = np.arange(1, 10).reshape(3, 3)

и вызвать эту
функцию:

np.random.shuffle(a)

то в массиве aбудут
переставлены только строки:

array(,

      
,

])

Вторая функция
возвращает случайную последовательность чисел, генерируя последовательность «на
лету»:

np.random.permutation(10) # array()

Рекомендация Numpy Форма

Атрибут формы всегда возвращает кортеж, который сообщает нам длину каждого измерения. Одномерный массив представляет собой вектор строки, и его форма – это одно значение, которое следует запястья. Одномерные массивы не имеют строк и столбцов, поэтому атрибут формы возвращает отдельный кортеж.

Давайте посмотрим на пример:

import numpy as np

#an one-dimensional NumPy array
arr = np.arange(10)

#print an array
print(arr)
# 

print(arr.shape)
# (10, )

Кодовый фрагмент также использует Numpy arange Функция для создания начального массива последующих значений от 0 до 9. Пожалуйста, найдите подробное обсуждение Numpy arange Функция в этом блоге Finxter Blog: https://blog.finxter.com/numpy-arange/ Отказ

Атрибут формы двумерного массива (также называемого матрицей) дает нам кортеж. Форма возвращает количество элементов вдоль каждого измерения, которое является количеством рядов и столбцов в двухмерном массиве.

# A two-dimensional NumPy array
import numpy as np

arr = np.array(, ])
print(arr.shape)
# (2, 5)

В следующем примере для формы трехмерных массивов.

# A three-dimensional array
import numpy as np

arr = np.array(, ,  ],, ,  ] ])
print(arr.shape)
# (2, 3, 4)

Требуется некоторая практика, чтобы понять кортеж формы для многомерных массивов. Размеры, представленные кортежом, читаются из наружу. Если вы соблюдаете скобки, самый простой кронштейн является частью основного синтаксиса для всего массива. В форме кортежа 2 представляет собой второй набор скобок. Если вы считаете их, вы увидите, что в этом измерении есть 2 элемента.

1-й элемент

2-й элемент

Каждый элемент содержит еще 3 элемента во втором измерении. Если вы думаете о вложенных списках, вы можете нарисовать аналогию. Эти элементы:

1-й элемент

2-й элемент

3-й элемент [

Наконец, номер 4 представляет количество элементов в третьем измерении. Это самые внутренние элементы. Например 0, 11, 15 и 16.

Вы хотите стать Numpy Master? Проверьте нашу интерактивную книгу головоломки Coffe Break Numpy И повысить свои навыки науки о данных! (Ссылка Amazon открывается на новой вкладке.)

Транспонирование и изменение формы матриц в numpy

Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.

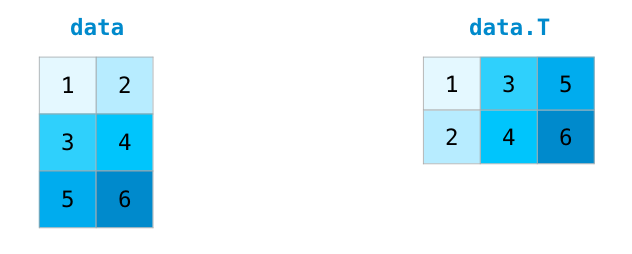
Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:

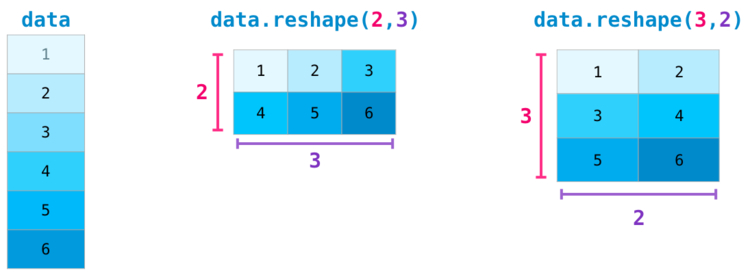
Еще больше размерностей NumPy

NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.

В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:

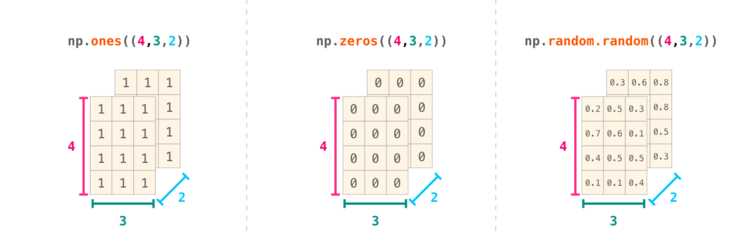
Shell

array(,
,
],

,
,
],

,
,
],

,
,
]])

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.)

Нарезка массива NumPy

Опять же, подобно стандартной библиотеке Python, NumPy также предоставляет нам операцию среза для массивов numpy, с помощью которой мы можем получить доступ к срезу массива элементов, чтобы получить соответствующий подмассив.

>>> b
array(,
       ])
>>> b
array()

На самом деле, это широко рекомендуемый способ использования массивов NumPy из-за высоко оптимизированного характера операций numpy. Поскольку собственные методы python довольно медленны по сравнению с ними, мы должны использовать только методы numpy для манипулирования массивами numpy. В результате чистые итерационные циклы Python и другие понимания списков не используются с numpy.

Дискретное преобразование Фурье (numpy.fft)¶

Прямое преобразование	Обратное преобразование	Описание
fft(a)	ifft(a)	одномерное дискретное преобразование Фурье
fft2(a)	ifft2(a)	двумерное дискретное преобразование Фурье
fftn(a)	ifftn(a)	многомерное дискретное преобразование Фурье
rfft(a)	irfft(a)	одномерное дискретное преобразование Фурье (действительные числа)
rfft2(a)	irfft2(a)	двумерное дискретное преобразование Фурье (действительные числа)
rfftn(a)	irfftn(a)	многомерное дискретное преобразование Фурье (действительные числа)
hfft(a)	ihfft(a)	преобразование Фурье сигнала с Эрмитовым спектром
fftfreq(n)		частоты дискретного преобразования Фурье
fftshift(a)	ifftshift(a)	преобразование Фурье со сдвигом нулевой компоненты в центр спектра

Коробчатые графики

Коробчатые диаграммы довольно информативны и полезны, особенно когда вам нужно показать слишком много из очень небольшого количества данных. Попробуем создать:

import random
import plotly
from numpy import *

N = 30.     # Number of boxes

# generate an array of rainbow colors by fixing the saturation and lightness of the HSL representation of colour
# and marching around the hue.
c = 

# Each box is represented by a dict that contains the data, the type,
# and the colour.
# Use list comprehension to describe N boxes, each with a different colour and
# with different randomly generated data:
data = [{
    'y': 3.5*sin(pi * i/N) + i/N+(1.5+0.5*cos(pi*i/N))*random.rand(10),
    'type':'box',
    'marker':{'color': c}
    } for i in range(int(N))]

# format the layout
layout = {'xaxis': {'showgrid':False,'zeroline':False, 'tickangle':60,'showticklabels':False},
          'yaxis': {'zeroline':False,'gridcolor':'white'},
          'paper_bgcolor': 'rgb(233,233,233)',
          'plot_bgcolor': 'rgb(233,233,233)',
          }

plotly.offline.plot(data)

Давайте посмотрим на результат этой программы:

Мы снова переместили указатель мыши на одну из точек, чтобы изучить дополнительную информацию об этой точке.

ПАРАМЕТРЫ МЕДИАНЫ NUMPY()

a: array_like

Параметр представляет входной массив или объекты, которые могут быть преобразованы в массив. Это, как правило, вход, из которого пользователь хочет найти медиану.

axis: int, последовательность int, none

Это параметр, по которому выполняется вся операция. По умолчанию он настроен на вычисление вдоль сплющенного массива.

< out: nsarray

Это необязательный параметр. Он должен иметь ту же форму и буфер, что и ожидаемый выходной массив.

Это еще один необязательный параметр. Если оно равно true, то для вычисления используется память входного массива. Это помогает нам сохранять память, когда мы не хотим ее сохранять. В этом случае не определено, что будет частично или полностью отсортировано. По умолчанию он установлен в значение “FALSE.”

Keepdims: bool

Это еще один необязательный параметр. Если он установлен в “TRUE”, то с помощью этого параметра результаты будут корректно транслироваться на входной массив.

ВЕРНУТЬ

медиана: ndarray

Он возвращает новый массив, содержащий результаты. Если входные данные содержат значения, меньшие, чем float64(позволяет хранить большее число), , то тип выходных данных-np.float64. В противном случае тип данных ввода и вывода один и тот же.

ПРИМЕР

Теперь давайте рассмотрим несколько примеров, которые помогут нам лучше понять эту концепцию.

import numpy as ppool.array()
print(ppool.median(a))
.array()
print(ppool.median(b))

Выход:

Здесь, в приведенном выше примере, мы использовали NumPy Median() для вычисления медианы. Во-первых, у нас есть импортированная библиотека NumPy. Далее мы определили массив. Наконец, мы использовали наш синтаксис, чтобы найти медиану для входного массива. Выше мы рассмотрели 2 различных массива, один из которых имеет нечетное число членов, а другой-четное число членов. Теперь давайте рассмотрим другой пример и немного поиграем с синтаксисом.

NumPy Медиана с

import numpy as ppool
a=,
   ,
   ,
   ]))

Выход:

В этом примере мы использовали шаги, аналогичные нашему первому примеру. Сначала импортируем массив, затем определяем массив. Но здесь мы имеем определенную ось, равную нулю. В этом случае мы получаем выход, эквивалентный . Теперь я объясню логику этого вывода. Как и в математике, программа упорядочивает значение в порядке возрастания для каждого же индекса подмассива. Как и порядок для нулевого значения индекса. Далее, поскольку число членов здесь четное, то требуется n/2-й и n/2+1-й члены массива 1 и 6. Затем вычислите среднее значение 2 слагаемых, которое дает нам наше медианное значение для этого индексного числа, например 3,5 для. Аналогично, процесс повторяется для каждого индексного номера.

NumPy Медиана с

import numpy as ppool
a=,
   ]))

Выход:

Здесь, в приведенном выше примере, мы видим, что рассматривали 2-мерный массив. Как всегда, сначала мы импортируем библиотеку NumPy. На следующем шаге мы определили наш 2-d массив. Здесь мы указали, что ось равна 1. В результате чего на выходе мы не получаем сплющенного массива. Далее он находит медиану для 2 суб-массивов. Благодаря чему мы получаем 5 и 6 в качестве медианы на выходе.

NumPy медианный фильтр

Медианный фильтр используется для обработки изображений. Медианный фильтр занимает интенсивность центрального пикселя. Он делает лучшую работу, чем средний фильтр при удалении. Он сохраняет края изображения, но не имеет дела с спекл-шумом. Спекл в основном обнаруживается в случае медицинских изображений и активен href=”https://en.wikipedia.org/wiki/Radar”>радарные изображения. href=”https://en.wikipedia.org/wiki/Radar”>радарные изображения.

Должен Читать

• Как Удалить Символ Из Строки Python
• Серия Фибоначчи в Python и программа чисел Фибоначчи
• ЧТО ТАКОЕ NUMPY DIFF? ВМЕСТЕ С ПРИМЕРАМИ
• NumPy log Function() | Что такое Numpy log в Python
• МЕТОДЫ ПРЕОБРАЗОВАНИЯ КОРТЕЖА В СТРОКУ В PYTHON

В этой статье мы рассмотрели медиану NumPy(). Мы рассмотрели его синтаксис и различные параметры. Для лучшего понимания мы также рассмотрели несколько примеров. В конце концов, мы можем сделать вывод, что NumPy Median помогает нам, вычисляя медиану для наших входных значений. Надеюсь, эта статья смогла развеять все ваши сомнения. Но в случае, если у вас все еще есть какие-либо нерешенные вопросы, не стесняйтесь писать их ниже в разделе комментариев. Прочитав это, почему бы не прочитать Numpy dot product далее.

Функции математической статистики

Последняя группа
общематематических функций, которую мы рассмотрим на этом занятии, отвечает за
вычисления статистических характеристик случайных величин. Основные из них,
следующие:

Название	Описание
np.median(x)	Вычисление медианы величин x
np.var(x)	Дисперсия величин x
np.std(x)	Среднеквадратическое отклонение величин x
np.corrcoef(x)	Линейный коэффициент корреляции Пирсона
np.correlate(x)	Вычисление кросс-корреляции
np.cov(x)	Вычисление ковариационной матрицы

Рассмотрим
работу этих функций. Предположим, имеются следующие векторы:

x = np.array(1, 4, 3, 7, 10, 8, 14, 21, 20, 23)
y = np.array(4, 1, 6, 9, 13, 11, 16, 19, 15, 22)

Эти числа будем
воспринимать как реализации случайных величин X и Y. Тогда, для
вычисления медианы СВX, можно воспользоваться функцией:

np.median(x) # 9.0

Для расчета
дисперсии и СКО, функциями:

np.var(x) # дисперсия СВX на основе реализации x
np.std(y) # СКО СВY на основе реализации y

Далее, чтобы
рассчитать коэффициент корреляции Пирсона, объединим массивыx и y построчно:

XY = np.vstack(x, y) # матрица 2x10

и выполним
функцию:

np.corrcoef(XY)

Результатом
будет матрица 2×2:

array(,

      
])

Как ее следует
интерпретировать? В действительности, это автоковариационная матрица вектора СВ:

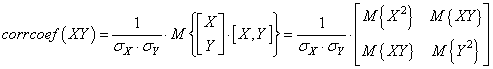
(В этой формуле
полагается, что СВX и Y центрированы, то есть имеют нулевое
математическое ожидание).

Если нужно
вычислить не нормированное МО, то есть, автоковариационную матрицу, то следует
воспользоваться функцией:

np.cov(XY) # ковариационная матрица размерностью 2x2

Наконец, для
вычисления взаимной корреляции между двумя векторамиx и y, используется
функция:

np.correlate(x, y) # array()

Более детальную
информацию по этим статистическим функциям можно найти в официальной
документации пакета NumPy:

Конечно, мы
рассмотрели далеко не все математические функции NumPy. На следующем
занятии продолжим эту тему и поговорим об умножении векторов и матриц, линейной
алгебре и множествах.

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

Начало работы с NumPy linspace()

Функция Numpy numpy.linspace() в основном используется для генерации линейной последовательности из диапазона чисел .

Обычно функция может использоваться для генерации последовательностей из диапазона чисел. Проблема с функцией numpy.arange() заключается в том, что она обеспечивает потерю точности в результате, если ей предоставляется аргумент плавающего типа.

Таким образом, функция numpy.linspace() может быть предпочтительнее.

Синтаксис:

numpy.linspace(start, stop, num = value, endpoint = True/False, retstep = False/True, dtype = None)

• : Это значение указывает начальную точку последовательности. Значение по умолчанию считается равным нулю(0).
• : Это значение указывает конечную точку последовательности.
• : Указывает количество шагов или элементов , которые будут сгенерированы между диапазоном запуска и остановки.

Пример:

import numpy
 
inp = numpy.linspace(1, 3, 5)
 
print('Linear Sequence:\n',inp)
print('Length of the sequence:\n')
print(len(inp))

Выход:

Linear Sequence:
 
Length of the sequence:
5

Параметр retstep Numpy linspace()

Параметр в основном представляет собой логическое значение . Если указано как True , он указывает размер шагов, выполняемых между каждым элементом для создания последовательности. Затем это приводит к последовательности в виде кортежа .

Пример:

import numpy 

inp = numpy.linspace(1, 3, num=5, retstep=True)
print(inp)
print("Length of the sequence:",len(inp))

Как упоминалось выше, когда передается в качестве аргумента методу linspace (), он генерирует кортеж в качестве вывода. Таким образом, длина кортежа будет 2, а не 6 !

Выход:

(array(), 0.5)
Length of the sequence: 2

Параметр конечной точки метода linspace()

Параметр является логическим значением. Если установлено значение False , он исключает последнее число последовательности в результате. Значение конечной точки по умолчанию – True .

Пример :

import numpy
 
inp = numpy.linspace(1, 3, 5, endpoint=False)
 
print('Sequence from 1 to 3:', inp)

Выход:

Sequence from 1 to 3: 

Параметр оси метода linspace()

Параметр axis в основном позволяет пользователю предоставить ось для хранения сгенерированных последовательностей . Параметр axis может применяться только в том случае, если start и endpoint данных имеют тип array .

Пример :

import numpy
 
inp1 = numpy.array(, ])
inp2 = numpy.array(, ])
 
op1 = numpy.linspace(inp1, inp2, 4, axis=0)
print(op1)

op2 = numpy.linspace(inp1, inp2, 2, axis=1)
print(op2)

Когда axis , он принимает ограничения последовательности от первой предоставленной оси. Пары подмассивов вместе с рассматриваются как ограничения для получения последовательности из isp1 в inp2 .

Когда axis , он использует последовательность столбцов для генерации элементов из заданного диапазона.

Выход:

  ]

 
  ]

 
  ]

 
  ]]



  ]

 
  ]]

Арифметические операции над массивами NumPy

Создадим два массива NumPy и продемонстрируем выгоду их использования.

Массивы будут называться и :

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать :

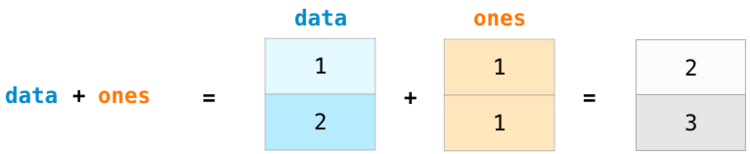
Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.

Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию :

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.