Библиотека numpy. полезные инструменты
Содержание:
- Добро пожаловать в NumPy!
- Установка NumPy
- Как импортировать NumPy
- В чем разница между списком Python и массивом NumPy?
- Что такое массив?
- Тригонометрические функции
- Линейная алгебра
- Транспонирование и изменение формы матриц в numpy
- Случайные величины (numpy.random)¶
- Примеры
- Рекомендация Numpy Форма
- Универсальные статистические функции
- Использование функции reshape()
- Полиномы (numpy.polynomial)¶
- Работа с матрицей с помощью NumPy
- Аргумент ключевого слова axis
- Вывод
Добро пожаловать в NumPy!
NumPy (NumericalPython) — это библиотека Python с открытым исходным кодом, которая используется практически во всех областях науки и техники. Это универсальный стандарт для работы с числовыми данными в Python, и он лежит в основе научных экосистем Python и PyData. В число пользователей NumPy входят все — от начинающих программистов до опытных исследователей, занимающихся самыми современными научными и промышленными исследованиями и разработками. API-интерфейс NumPy широко используется в пакетах Pandas, SciPy, Matplotlib, scikit-learn, scikit-image и в большинстве других научных и научных пакетов Python.
Библиотека NumPy содержит многомерный массив и матричные структуры данных (дополнительную информацию об этом вы найдете в следующих разделах). Он предоставляет ndarray, однородный объект n-мерного массива, с методами для эффективной работы с ним. NumPy может использоваться для выполнения самых разнообразных математических операций над массивами. Он добавляет мощные структуры данных в Python, которые гарантируют эффективные вычисления с массивами и матрицами, и предоставляет огромную библиотеку математических функций высокого уровня, которые работают с этими массивами и матрицами.
Узнайте больше о NumPy здесь!
GIF черезgiphy
Установка NumPy
Чтобы установить NumPy, я настоятельно рекомендую использовать научный дистрибутив Python. Если вам нужны полные инструкции по установке NumPy в вашей операционной системе, вы можетенайти все детали здесь,
Если у вас уже есть Python, вы можете установить NumPy с помощью
conda install numpy
или
pip install numpy
Если у вас еще нет Python, вы можете рассмотреть возможность использованияанаконда, Это самый простой способ начать. Преимущество этого дистрибутива в том, что вам не нужно слишком беспокоиться об отдельной установке NumPy или каких-либо основных пакетов, которые вы будете использовать для анализа данных, таких как pandas, Scikit-Learn и т. Д.
Если вам нужна более подробная информация об установке, вы можете найти всю информацию об установке наscipy.org,
фотоАдриеннотPexels
Если у вас возникли проблемы с установкой Anaconda, вы можете ознакомиться с этой статьей:
Как импортировать NumPy
Каждый раз, когда вы хотите использовать пакет или библиотеку в своем коде, вам сначала нужно сделать его доступным.
Чтобы начать использовать NumPy и все функции, доступные в NumPy, вам необходимо импортировать его. Это можно легко сделать с помощью этого оператора импорта:
import numpy as np
(Мы сокращаем «numpy» до «np», чтобы сэкономить время и сохранить стандартизированный код, чтобы любой, кто работает с вашим кодом, мог легко его понять и запустить.)
В чем разница между списком Python и массивом NumPy?
NumPy предоставляет вам огромный выбор быстрых и эффективных числовых опций. Хотя список Python может содержать разные типы данных в одном списке, все элементы в массиве NumPy должны быть однородными. Математические операции, которые должны выполняться над массивами, были бы невозможны, если бы они не были однородными.
Зачем использовать NumPy?
фотоPixabayотPexels
Массивы NumPy быстрее и компактнее, чем списки Python. Массив потребляет меньше памяти и намного удобнее в использовании. NumPy использует гораздо меньше памяти для хранения данных и предоставляет механизм задания типов данных, который позволяет оптимизировать код еще дальше.
Что такое массив?
Массив является центральной структурой данных библиотеки NumPy. Это таблица значений, которая содержит информацию о необработанных данных, о том, как найти элемент и как интерпретировать элемент. Он имеет сетку элементов, которые можно проиндексировать в Все элементы имеют одинаковый тип, называемыймассив dtype(тип данных).
Массив может быть проиндексирован набором неотрицательных целых чисел, логическими значениями, другим массивом или целыми числами.рангмассива это количество измерений.формамассива — это кортеж целых чисел, дающий размер массива по каждому измерению.
Одним из способов инициализации массивов NumPy является использование вложенных списков Python.
a = np.array(, , ])
Мы можем получить доступ к элементам в массиве, используя квадратные скобки. Когда вы получаете доступ к элементам, помните, чтоиндексирование в NumPy начинается с 0, Это означает, что если вы хотите получить доступ к первому элементу в вашем массиве, вы получите доступ к элементу «0».
print(a)
Выход:
Тригонометрические функции
Конечно, любой
состоятельный математический пакет должен иметь в своем составе
тригонометрические функции и NumPyздесь не исключение. Наиболее
употребительные из них приведены в следующей таблице:
|
Название |
Описание |
|
np.sin(x) |
Вычисление |
|
np.cos(x) |
Вычисление |
|
np.tan(x) |
Вычисление |
|
np.arccos(x) |
Арккосинус |
|
np.arcsin(x) |
Арксинус |
|
np.arctan(x) |
Арктангенс |
Их использование
также вполне очевидно. На входе они могут принимать массив, список или число.
Если это угол, то он представляется в радианах. Например:
a = np.linspace(, np.pi, 10) res1 = np.sin(a) # возвращает массив синусов углов np.sin(np.pi/3) np.cos(, 1.57, 3.17) res2 = np.cos(a) # возвращает массив косинусов углов np.arcsin(res1) # возвращает арксинусы от значений res1
Причем, все эти
функции работают быстрее аналогичных функций языка Python. Поэтому, при
использовании библиотеки NumPy предпочтение лучше отдавать именно ей,
а не языку Python при
тригонометрических вычислениях.
Линейная алгебра
SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.
Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.
Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.
Этот метод ожидает входную матрицу и вектор правой части:
# Import required modules/ libraries
import numpy as np
from scipy import linalg
# We are trying to solve a linear algebra system which can be given as:
# 1x + 2y =5
# 3x + 4y =6
# Create input array
A= np.array(,])
# Solution Array
B= np.array(,])
# Solve the linear algebra
X= linalg.solve(A,B)
# Print results
print(X)
# Checking Results
print("\n Checking results, following vector should be all zeros")
print(A.dot(X)-B)

Транспонирование и изменение формы матриц в numpy
Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.
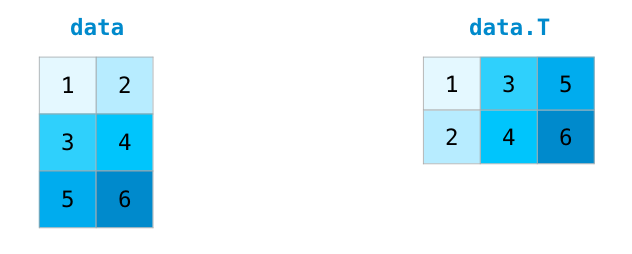
Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:
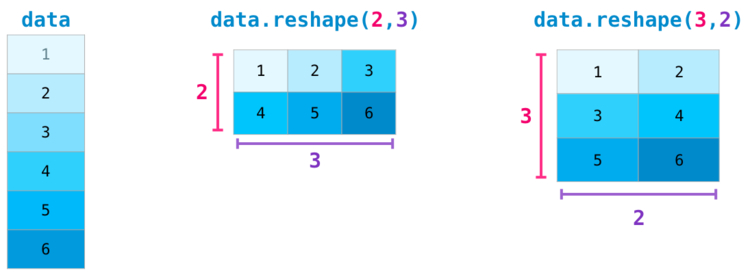
Еще больше размерностей NumPy
NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.

В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:
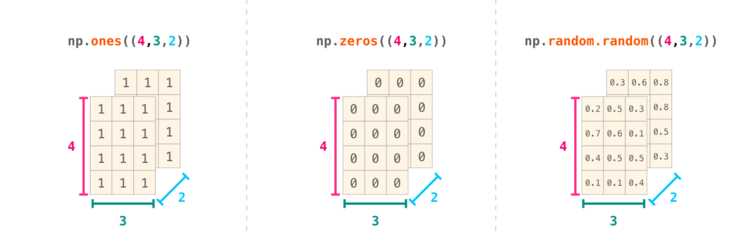
Shell
array(,
,
],
,
,
],
,
,
],
,
,
]])
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.) |
Случайные величины (numpy.random)¶
В модуле numpy.random собраны функции для генерации массивов случайных чисел различных распределений и свойств.
Их можно применять для математического моделирования. Функция random() создает массивы из псевдослучайных чисел,
равномерно распределенных в интервале (0, 1). Функция RandomArray.randint() для получения массива равномерно
распределенных чисел из заданного интервала и заданной формы. Можно получать и случайные перестановки с помощью
RandomArray.permutation(). Доступны и другие распределения для получения массива нормально распределенных величин
с заданным средним и стандартным отклонением:
Следующая таблица приводит основные функции модуля.
| Команда | Описание |
|---|---|
| rand(d0, d1, …, dn) | набор случайных чисел заданной формы |
| randn() | набор (или наборы) случайных чисел со стандартным нормальным распределением |
| randint(low) | случайные целые числа от low (включая) до high (не включая). |
| random_integers(low) | случайные целые числа между low и high (включая). |
| random_sample() | случайные рациональные числа из интервала [0.0, 1.0). |
| bytes(length) | случайные байты |
| shuffle(x) | тасовка элементов последовательностина месте |
| permutation(x) | возвращает последовательность, переставленных случайным образом элементов |
| seed() | перезапуск генератора случайных чисел |
| beta(a, b) | числа с Бетта- распределением \(f(x,\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) \(B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\) |
| binomial(n, p) | числа с биномиальным распределением \(P(N)= \left( \frac{n}{N} \right) p^N (1-p)^{n-N}\) |
| chisquare(df) | числа с распределением хи-квадрат \(p(x)=\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2-1} e^{-x/2}\) |
| mtrand.dirichlet(alpha) | числа с распределением Дирихле (alpha – массив параметров). |
| exponential() | числа с экспоненциальным распределением \(f(x,\frac{1}{\beta})=\frac{1}{\beta}exp(-\frac{x}{\beta})\) |
| f(dfnum, dfden) | числа с F распределением (dfnum – число степеней свободы числителя > 0; dfden –число степеней свободы знаменателя >0.) |
| gamma(shape) | числа с Гамма — распределением |
| geometric(p) | числа с геометрическим распределением |
| gumbel() | числа с распределением Гумбеля |
| hypergeometric(ngood, nbad, nsample) | числа с гипергеометрическим распределением (n = ngood, m = nbad, and N = number of samples) |
| laplace() | числа с распределением Лапласа |
| logistic() | числа с логистическим распределением |
| lognormal() | числа с логарифмическим нормальным распределением |
| logseries(p) | числа с распределением логарифмического ряда |
| multinomial(n, pvals) | числа с мультиномиальным распределением |
| multivariate_normal(mean, cov) | числа с мульти нормальным распределением (mean – одномерный массив средних значений; cov – двухмерный симметричный, полож. определенный массив (N, N) ковариаций |
| negative_binomial(n, p) | числа с отрицательным биномиальным распределением |
| noncentral_chisquare(df, nonc) | числа с нецентральным распределением хи-квадрат |
| noncentral_f(dfnum, dfden, nonc) | числа с нецентральным F распределением (dfnum — целое > 1; dfden – целое > 1; nonc : действительное >= 0) |
| normal() | числа с нормальным распределением |
| pareto(a) | числа с распределением Паретто |
| poisson() | числа с распределением Пуассона |
| power(a) | числа со степенным распределением |
| rayleigh() | числа с распределением Релея |
| standard_cauchy() | числа со стандартным распределением Коши |
| standard_exponential() | числа со стандартным экспоненциальным распределением |
| standard_gamma(shape) | числа с гамма- распределением |
| standard_normal() | числа со стандартным нормальным распределением (среднее=0, сигма=1). |
| standard_t(df) | числа со стандартным распределением Стьюдента с df степенями свободы |
| triangular(left, mode, right) | числа из треугольного распределения |
| uniform() | числа с равномерным распределением |
| vonmises(mu, kappa) | числа с распределением Майсеса (I- модифицированная функция Бесселя) |
| wald(mean, scale) | числа с распределением Вальда |
| weibull(a) | числа с распределением Вайбулла |
| zipf(a) | числа с распределением Зипфа (зетта функция Римана) |
Примеры
Простой пример применительно применительно к массиву NUMPY:
>>> import numpy as np >>> a = np.array(, ]) >>> np.shape(a) (2, 2)
Вы импортируете Numpy Library и создаете двумерный массив из списка списков. Если вы передаете множество массива в функцию формы, она возвращает кортеж с двумя значениями). Каждое измерение хранит количество элементов в этом измерении). Как это квадратичная матрица 2 × 2, результат (2,2).
Следующая форма является еще одним примером многомерного массива:
>>> b = np.array(, ])
>>> b
array(,
])
>>> b.shape
(2, 4)
>>> np.shape(b)
(2, 4)
Форма сейчас с двумя рядами и четырьмя колоннами.
np.shape () vs array.shape
Обратите внимание, что результат и одинаково, если это небольшой массив. Если Разве немаловая массива не в списке, вы не можете использовать В качестве списков нет атрибута формы
Давайте посмотрим на этот пример:
>>> b = , ] >>> np.shape(b) (2, 4)
Функция возвращает одинаковую форму кортежа – даже если вы передаете вложенный список в функцию вместо Numpy Array.
Но если вы попытаетесь получить доступ к списку .shape Атрибут, numpy бросает следующую ошибку:
>>> b.shape
Traceback (most recent call last):
File "", line 1, in
b.shape
AttributeError: 'list' object has no attribute 'shape'#9>
Итак, разница между и Это то, что первое можно использовать для всех видов Array_Like Объекты, в то время как последний можно использовать только для применения ToMpy с атрибут.
Рекомендация Numpy Форма
Атрибут формы всегда возвращает кортеж, который сообщает нам длину каждого измерения. Одномерный массив представляет собой вектор строки, и его форма – это одно значение, которое следует запястья. Одномерные массивы не имеют строк и столбцов, поэтому атрибут формы возвращает отдельный кортеж.
Давайте посмотрим на пример:
import numpy as np #an one-dimensional NumPy array arr = np.arange(10) #print an array print(arr) # print(arr.shape) # (10, )
Кодовый фрагмент также использует Numpy arange Функция для создания начального массива последующих значений от 0 до 9. Пожалуйста, найдите подробное обсуждение Numpy arange Функция в этом блоге Finxter Blog: https://blog.finxter.com/numpy-arange/ Отказ
Атрибут формы двумерного массива (также называемого матрицей) дает нам кортеж. Форма возвращает количество элементов вдоль каждого измерения, которое является количеством рядов и столбцов в двухмерном массиве.
# A two-dimensional NumPy array import numpy as np arr = np.array(, ]) print(arr.shape) # (2, 5)
В следующем примере для формы трехмерных массивов.
# A three-dimensional array import numpy as np arr = np.array(, , ],, , ] ]) print(arr.shape) # (2, 3, 4)
Требуется некоторая практика, чтобы понять кортеж формы для многомерных массивов. Размеры, представленные кортежом, читаются из наружу. Если вы соблюдаете скобки, самый простой кронштейн является частью основного синтаксиса для всего массива. В форме кортежа 2 представляет собой второй набор скобок. Если вы считаете их, вы увидите, что в этом измерении есть 2 элемента.
1-й элемент
2-й элемент
Каждый элемент содержит еще 3 элемента во втором измерении. Если вы думаете о вложенных списках, вы можете нарисовать аналогию. Эти элементы:
1-й элемент
2-й элемент
3-й элемент [
Наконец, номер 4 представляет количество элементов в третьем измерении. Это самые внутренние элементы. Например 0, 11, 15 и 16.
Вы хотите стать Numpy Master? Проверьте нашу интерактивную книгу головоломки Coffe Break Numpy И повысить свои навыки науки о данных! (Ссылка Amazon открывается на новой вкладке.)
Универсальные статистические функции
Помимо тригонометрических функций, Python NumPy также предлагает нам универсальные статистические функции. Некоторые из них перечислены ниже:
- функция numpy.amin () : Представляет минимальное значение из массива.
- функция numpy.amax () : Представляет максимальное значение из массива.
- функция numpy.ptp () : Представляет диапазон значений массива по оси, который вычисляется путем вычитания минимального значения из максимального значения.
- функция numpy.average () : вычисляет среднее значение элементов массива.
Пример:
import numpy as np
data = np.array()
print('Minimum and maximum data values from the array: ')
print(np.amin(data))
print(np.amax(data))
print('Range of the data: ')
print(np.ptp(data))
print('Average data value of the array: ')
print(np.average(data))
Выход:
Minimum and maximum data values from the array: 7.9 56.0 Range of the data: 48.1 Average data value of the array: 27.025000000000002
Использование функции reshape()
Первым делом, прежде чем попрактиковаться в использовании данной функции, вам следует импортировать библиотеку NumPy. После этого можно приступать к работе.
Далее мы покажем различные варианты использования функции .
Пример 1: преобразование одномерного массива в двумерный
Итак, давайте разберем, как с помощью функции преобразовать одномерный массив в двумерный.
В этом сценарии для создания одномерного массива из 10 элементов используется функция .
Первая функция используется для преобразования одномерного массива в двумерный, состоящий из 2 строк и 5 столбцов. Здесь функция вызывается с использованием имени модуля .
А вторая функция используется для преобразования одномерного массива в двумерный, состоящий из 5 строк и 2 столбцов. Здесь уже функция вызывается с использованием массива NumPy с именем .
import numpy as np
np_array = np.arange(10)
print("Исходный массив : \n", np_array)
new_array = np.reshape(np_array, (2, 5))
print("\n Измененный массив с 2 строками и 5 столбцами : \n", new_array)
new_array = np_array.reshape(5, 2)
print("\n Измененный массив с 5 строками и 2 столбцами : \n", new_array)
Если вы запустите описанную выше программу, то получите результат, как на следующем скриншоте. Первый показывает исходный массив, а второй и третий выводят преобразованные массивы.

Пример 2: преобразование одномерного массива в трехмерный
Теперь давайте посмотрим, как при помощи функции преобразовать одномерный массив в трехмерный.
Воспользуемся функцией для создания одномерного массива из 12 элементов.
Функция преобразует созданный одномерный массив в трехмерный размером 2х2х3. Здесь функция вызывается с использованием NumPy-массива .
import numpy as np
np_array = np.array()
print("Исходный массив : \n", np_array)
new_array = np_array.reshape(2, 2, 3)
print("\n Преобразованный 3D массив : \n", new_array)
Выполнив данный код, вы получите следующий вывод. Как и в прошлый раз, первый показывает изначальный массив, второй – преобразованный массив.

Пример 3: изменение формы массива NumPy с учетом порядка
Как вы помните, у функции есть третий — опциональный — аргумент, задающий порядок индексации. Давайте посмотрим, как он применяется на практике.
Как и в первом примере, воспользуемся функцией для создания одномерного массива из 15 элементов.
Первая функция используется для создания двумерного массива из 3 строк и 5 столбцов с упорядочением в стиле C. В то время как вторая функция используется для создания двумерного массива из 3 строк и 5 столбцов с упорядочением в стиле Фортрана.
import numpy as np
np_array = np.arange(15)
print("Исходный массив : \n", np_array)
new_array1 = np.reshape(np_array, (3, 5), order='C')
print("\n Преобразованный 2D массив, упорядоченный в стиле С : \n", new_array1)
new_array2 = np.reshape(np_array, (3, 5), order='F')
print("\n Преобразованный 2D массив, упорядоченный в стиле Фортрана : \n", new_array2)
Давайте выполним наш код. Вот, что мы получим. Как и раньше, первый показывает исходный массив значений. Второй показывает значения массива, упорядоченного по строкам. Третий – упорядоченного по столбцам.

Полиномы (numpy.polynomial)¶
Модуль полиномов обеспечивает стандартные функции работы с полиномами разного вида. В нем реализованы полиномы
Чебышева, Лежандра, Эрмита, Лагерра. Для полиномов определены стандартные арифметические функции ‘+’, ‘-‘, ‘*’, ‘//’,
деление по модулю, деление с остатком, возведение в степень и вычисление значения полинома
Важно задавать область
определения, т.к. часто свойства полинома (например при интерполяции) сохраняются только на определенном интервале.
В зависимости от класса полинома, сохраняются коэффициенты разложения по полиномам определенного типа, что позволяет
получать разложение функций в ряд по полиномам разного типа
| Типы полиномов | Описание |
|---|---|
| Polynomial(coef) | разложение по степеням «x» |
| Chebyshev(coef) | разложение по полиномам Чебышева |
| Legendre(coef) | разложение по полиномам Лежандра |
| Hermite(coef) | разложение по полиномам Эрмита |
| HermiteE(coef) | разложение по полиномам Эрмита_Е |
| Laguerre(coef) | разложение по полиномам Лагерра |
- coef – массив коэффициентов в порядке увеличения
- domain – область определения проецируется на окно
- window – окно. Сдвигается и масштабируется до размера области определения
Некоторые функции (например интерполяция данных) возвращают объект типа полином. У этого объекта есть набор методов,
позволяющих извлекать и преобразовывать данные.
| Методы полиномов | Описание |
|---|---|
| __call__(z) | полином можно вызвать как функцию |
| convert() | конвертирует в полином другого типа, с другим окном и т.д |
| copy() | возвращает копию |
| cutdeg(deg) | обрезает полином до нужной степени |
| degree() | возвращает степень полинома |
| deriv() | вычисляет производную порядка m |
| fit(x, y, deg) | формирует полиномиальную интерполяцию степени deg для данных (x,y) по методу наименьших квадратов |
| fromroots(roots) | формирует полином по заданным корням |
| has_samecoef(p) | проверка на равенство коэффициентов. |
| has_samedomain(p) | проверка на равенство области определения |
| has_samewindow(p) | проверка на равенство окна |
| integ() | интегрирование |
| linspace() | возвращает x,y — значения на равномерной сетке по области определения |
| mapparms() | возвращает коэффициенты масштабирования |
| roots() | список корней |
| trim() | создает полином с коэффициентами большими tol |
| truncate(size) | ограничивает ряд по количеству коеффициентов |
- p – полином
- x, y – набор данных для аппроксимации
- deg – степень полинома
- domain – область определения
- rcond – относительное число обусловленности элементы матрицы интерполяции с собственными значениями меньшими данного будут отброшены.
- full – выдавать дополнительную информацию о качестве полинома
- w – веса точек
- window – окно
- roots – набор корней
- m – порядок производной (интеграла)
- k – константы интегрирования
- lbnd – нижняя граница интервала интегрирования
- n – число точек разбиения
- size – число ненулевых коэффициентов
Работа с матрицей с помощью NumPy
Мы можем выполнять все операции с матрицей, используя numpy.array(), такие как сложение, вычитание, транспонирование, нарезание матрицы и т. д.
Добавление матрицы
Мы создадим две матрицы с помощью функции numpy.array() и добавим их с помощью оператора +. Давайте разберемся в следующем примере.
Пример —
import numpy as np
mat1 = np.array(, , ])
mat2 = np.array(, , ])
mat3 = mat1 + mat2
print("The matrix addition is: ")
print(mat3)
Выход:
The matrix addition is: ]
Умножение
Мы будем использовать метод numpy.dot() для умножения обеих матриц. Это точечное умножение матриц mat1 и mat2, обрабатывает 2D-массив и выполняет умножение.
Пример —
import numpy as np
mat1 = np.array(, ])
mat2 = np.array(, ])
mat3 = mat1.dot(mat2)
print("The matrix is:")
print(mat3)
Выход:
The matrix is: ]
Нарезка элементов
Мы можем разрезать элемент матрицы, как в стандартном списке Python. Нарезка возвращает элемент на основе индекса начала / конца. Мы также можем сделать отрицательную нарезку. Синтаксис приведен ниже.
Синтаксис —
arr
Arr представляет имя матрицы. По умолчанию начальный индекс равен 0, например — , это означает, что начальный индекс равен 0. Если мы не предоставим конечное значение, он будет учитывать длину массива. Мы можем передавать отрицательные значения индекса как в начало, так и в конец. В следующем примере мы применим нарезку в обычном массиве, чтобы понять, как она работает.
Пример —
import numpy as np arr = np.array() print(arr) # It will print the elements from 2 to 4 print(arr) # It will print the elements from 0 to 3 print(arr) # It will print the elements from 3 to length of the array.
Выход:
Теперь мы реализуем нарезку по матрице. Для выполнения следуйте синтаксису ниже.
Mat1
В приведенном выше синтаксисе:
- Первое начало / конец представляет строки, которые означают выбор строк матрицы.
- Первое начало / конец представляет столбцы, которые означают выбор столбца матрицы.
Мы будем выполнять нарезку в приведенной ниже матрице.
mat1 = np.array(,
,
,
])
Вышеупомянутая матрица состоит из четырех строк. В 0-м ряду есть , в 1-й строке — и так далее. В нем пять столбцов. Рассмотрим на примере.
Пример —
import numpy as np
mat1 = np.array(,
,
,
])
print(mat1)
Выход:
]
Объяснение:
В приведенном выше примере мы напечатали первую и вторую строки и нарезали первый, второй и третий столбцы. Согласно синтаксису нарезки мы можем получить любые строки и столбцы.
Пример — печать первой строки и всех столбцов:
import numpy as np
mat1 = np.array(,
,
,
])
print(mat1)
Выход:
]
Пример — печать строк матрицы:
import numpy as np mat1 = np.array(, , ]) print(mat1) #first row print(mat1) # the second row print(mat1) # -1 will print the last row
Выход:
Аргумент ключевого слова axis
Это устанавливает axis для сохранения образцов. Он используется только в том случае, если начальная и конечная точки относятся к типу данных массива.
По умолчанию (axis = 0) образцы будут располагаться вдоль новой оси, вставленной в начало. Мы можем использовать axis = -1, чтобы получить ось в конце.
import numpy as np p = np.array(, ]) q = np.array(, ]) r = np.linspace(p, q, 3, axis=0) print(r) s = np.linspace(p, q, 3, axis=1) print(s)
Вывод
array(,
],
,
],
,
]])
array(,
,
],
,
,
]])
В первом случае, поскольку axis = 0, мы берем пределы последовательности от первой оси.
Здесь пределы – это пары подмассивов и , а также и , берущие элементы из первой оси p и q. Теперь мы сравниваем соответствующие элементы из полученной пары, чтобы сгенерировать последовательности.
Таким образом, последовательности , ] для первой строки и ], ] для второй пары (строки), которая оценивается и объединяется для формирования , ], , ], , ]],
Во втором случае будут вставлены новые элементы в axis = 1 или столбцы. Таким образом, новая ось будет создана через последовательности столбцов. вместо последовательностей строк.
Последовательности с по и по рассматриваются и вставляются в столбцы результата, в результате чего получается , , ], , , ]].
Будучи генератором линейной последовательности, функция numpy.arange() в Python используется для генерации последовательности чисел в линейном пространстве с равномерным размером шага.
Это похоже на другую функцию, numpy.linspace() в Python, которая также генерирует линейную последовательность с одинаковым размером шага.
Давайте разберемся, как мы можем использовать эту функцию для генерации различных последовательностей.
Вывод
В заключение эта статья предоставляет вам всю информацию о функции Numpy variance в Python. Функция дисперсии используется для нахождения дисперсии заданного набора данных. Импорт модуля Numpy дает доступ к созданию ndarray и выполнению таких операций, как среднее стандартное отклонение. Более того, дисперсия над ним осуществляется с помощью специальных функций, встроенных в сам модуль Numpy. Вы можете обратиться к приведенным выше примерам для любых запросов, касающихся функции Numpy var() в Python.
Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.
Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.