Matlab

Description

performs
a logical OR of arrays and and
returns an array containing elements set to either logical 1 ()
or logical 0 (). An element of the output
array is set to logical 1 () if either or contain
a nonzero element at that same array location. Otherwise, the array
element is set to 0.

For bit-wise logical OR operations, see .

is
an alternate way to execute , but is rarely
used. It enables operator overloading for classes.

Examples

Locate Zeros in Matrices

Open Live Script

Find the logical OR of two matrices. The result contains logical () where either matrix contains a nonzero value. The zeros in the result indicate spots where both arrays have a value of zero.

A = 

A = 3×3

     5     7     0
     0     2     9
     5     0     0

B = 

B = 3×3

     6     6     0
     1     3     5
    -1     0     0

A | B

ans = 3x3 logical array

   1   1   0
   1   1   1
   1   0   0

Truth Table for Logical OR

Open Live Script

Create a truth table for .

A = 

A = 1x2 logical array

   1   0

B = 

B = 2x1 logical array

   1
   0

C = A|B

C = 2x2 logical array

   1   1
   1   0

Input Arguments

, — Operandsscalars | vectors | matrices | multidimensional arrays

Operands, specified as scalars, vectors, matrices, or multidimensional
arrays. Inputs and must either be
the same size or have sizes that are compatible (for example,
is an -by-
matrix and is a scalar or
-by- row vector). For more
information, see Compatible Array Sizes for Basic Operations.

Data Types: | | | | | | | | | |

Tips

• Matlab r2014a полная установка скачать бесплатно

  You can chain together several logical operations,
  for example, .

• The symbols and perform different
  operations in MATLAB. The element-wise OR operator described here is
  . The short-circuit OR operator is
  .

• When you use the element-wise and
  operators in the context of an or
  loop expression (and only in that context), they
  use short-circuiting to evaluate expressions. Otherwise, you must specify
  or to opt-in to
  short-circuiting behavior. See for more information.

Compatibility Considerations

Implicit expansion change affects arguments for operators

Behavior changed in R2016b

Starting in R2016b with the addition of implicit expansion, some combinations of arguments for basic operations that previously returned errors now produce results. For example, you previously could not add a row and a column vector, but those operands are now valid for addition. In other words, an expression like previously returned a size mismatch error, but now it executes.

If your code uses element-wise operators and relies on the errors that MATLAB previously returned for mismatched sizes, particularly within a / block, then your code might no longer catch those errors.

For more information on the required input sizes for basic array operations, see Compatible Array Sizes for Basic Operations.

Extended Capabilities

C/C++ Code GenerationGenerate C and C++ code using MATLAB Coder.

Thread-Based EnvironmentRun code in the background using MATLAB or accelerate code with Parallel Computing Toolbox .

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

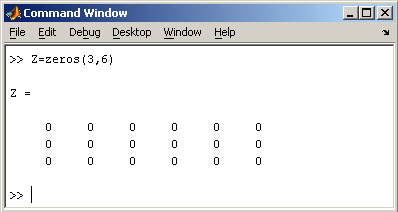
2.4. Создание матриц специального вида

Заполнение прямоугольной
матрицы нулями производится встроенной
функцией zeros

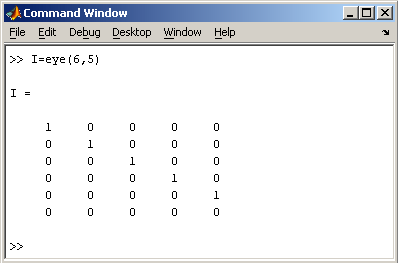
Единичная
матрица создается при помощи функции eye

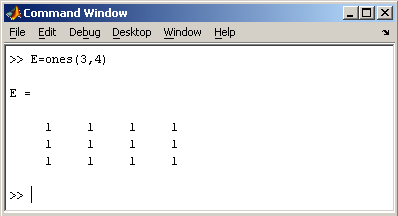
Матрица,
состоящая из единиц, образуется в
результате вызова функции ones

MatLab
предоставляет возможность заполнения
матриц случайными числами. Результатом
функции rand
является матрица чисел, равномерно
распределенных между нулем и единицей, а
функции randn
— матрица чисел, распределенных по
нормальному закону с нулевым средним и
единичной дисперсией. 

Функция
diag
формирует диагональную матрицу из
вектора, располагая элементы по
диагонали.

4.5 Печать графиков

Пункт Print в меню
File и команда print
печатают графику MatLab. Меню Print
вызывает диалоговое окно, которое
позволяет выбирать общие стандартные
варианты печати. Команда print
обеспечивает большую гибкость при
выводе выходных данных и позволяет
контролировать печать из М-файлов.
Результат может быть послан прямо на
принтер, выбранный по умолчанию, или
сохранен в заданном файле.

5. Примеры программ 

В этом разделе приведены
наиболее употребительные алгоритмы,
используемые при анализе многомерных
данных. Рассмотрены как простейшие
методы преобразования данных так и
алгоритмы для анализа данных — PCA, PLS.

1.1. Рабочая среда MatLab

Чтобы запустить программу дважды
щелкните на иконку . 
Перед Вами откроется рабочая среда,
изображенная на рисунке.

Рабочая среда MatLab 6.х немного
отличается от рабочей среды предыдущих
версий, она имеет более удобный
интерфейс для доступа ко многим
вспомогательным элементам

Рабочая среда MatLab 6.х содержит
следующие элементы:

• панель инструментов с кнопками и
  раскрывающимся списком;

• окно с вкладками Launch
  Pad и Workspace,
  из которого можно получить доступ к
  различным модулям ToolBox
  и к содержимому рабочей среды;

• окно с вкладками Command
  History и Current
  Directory, предназначенное
  для просмотра и повторного вызова
  ранее введенных команд, а также для
  установки текущего каталога;

• командное окно, в котором находится
  приглашение к вводу
  и мигающий вертикальный курсор;

• строку состояния.

Если в рабочей среде MatLab 6.х
отсутствуют некоторые окна, приведенные
на рисунке, то следует в меню View
выбрать соответствующие пункты: Command
Window, Command
History, Current
Directory, Workspase,
Launch Pad.

Команды следует набирать в командном
окне. Символ ,
обозначающий приглашение к вводу
командной строки, набирать не нужно. Для
просмотра рабочей области удобно
использовать полосы скроллинга или
клавиши Home, End,
для перемещения влево или вправо, и PageUp,
PageDown для
перемещения вверх или вниз. Если вдруг
после перемещения по рабочей области
командного окна пропала командная
строка с мигающим курсором, просто
нажмите Enter.

Важно помнить, что набор любой команды
или выражения должен заканчиваться
нажатием на Enter,
для того, чтобы программа MatLab выполнила
эту команду или вычислила выражение

2.1. Скаляры, векторы и матрицы

В MatLab можно использовать
скаляры, векторы и матрицы. Для ввода
скаляра достаточно приписать его
значение какой-то переменной, например

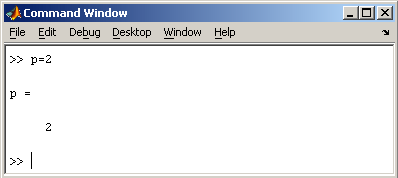
Заметим, что MatLab различает
заглавные и прописные буквы, так что p
и P — это разные переменные. Для
ввода массивов (векторов или матриц) их
элементы заключают в квадратные скобки.
Так для ввода вектора-строки размером 1×3,
используется следующая команда, в
которой элементы строки отделяются
пробелами или запятыми.

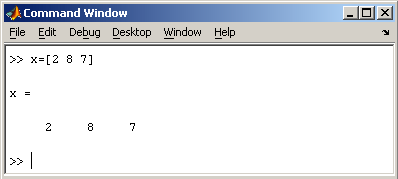
При вводе вектора-столбца
элементы разделяют точкой с запятой.
Например,

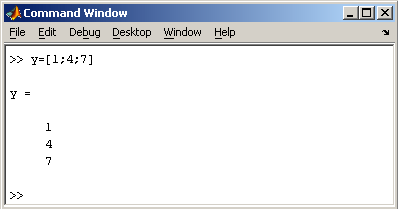
Вводить
небольшие по размеру матрицы удобно
прямо из командной строки. При вводе
матрицу можно рассматривать как вектор-столбец,
каждый элемент которого является вектором-строкой.

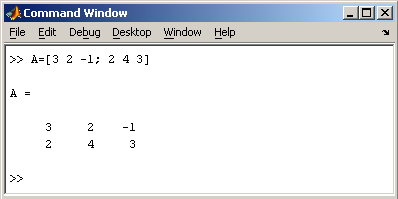
или матрицу можно трактовать
как вектор строку, каждый элемент
которой является вектором-столбцом.

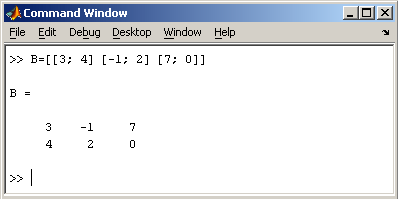
2.2. Доступ к элементам

Доступ к элементам матриц
осуществляется при помощи двух
индексов — номеров строки и столбца,
заключенных в круглые скобки, например
команда B(2,3)
выдаст элемент второй строки и
третьего столбца матрицы B. Для
выделения из матрицы столбца или
строки следует в качестве одного из
индексов использовать номер столбца
или строки матрицы, а другой индекс
заменить двоеточием. Например, запишем
вторую строку матрицы A в вектор
z

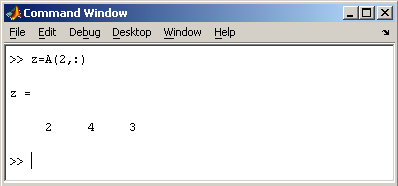
Также можно осуществлять
выделение блоков матриц при помощи
двоеточия. Например, выделим из матрицы
P блок отмеченный цветом

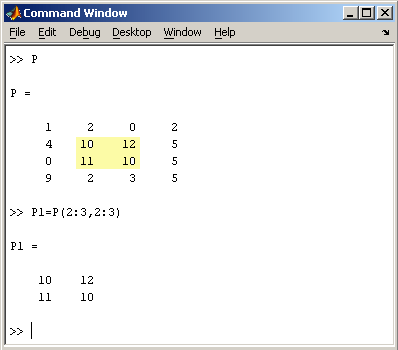
Если необходимо посмотреть
переменные рабочей среды, в командной
строке необходимо набрать команду whos.

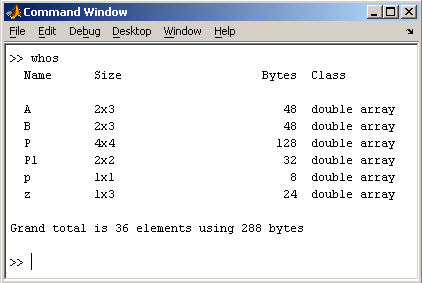
Видно,
что в рабочей среде содержатся один
скаляр (p), четыре матрицы (A, B, P,
P1) и вектор-строка (z).

4.3. Файл-функция

Рассмотренная выше файл-программа
является только последовательностью
команд MatLab, она не имеет входных и
выходных аргументов. Для использования
численных методов и при
программировании собственных
приложений в MatLab необходимо уметь
составлять файл-функции, которые
производят необходимые действия с
входными аргументами и возвращают
результат действия в выходных
аргументах. Разберем несколько простых
примеров, позволяющих понять работу с
файл-функциями. 

Проводя предобработку данных
многомерного анализа хемометрики
часто применяет . Имеет
смысл один раз написать файл-функцию, а
потом вызывать его всюду, где
необходимо производить центрирование.
Откройте в редакторе М-файлов новый
файл и наберите

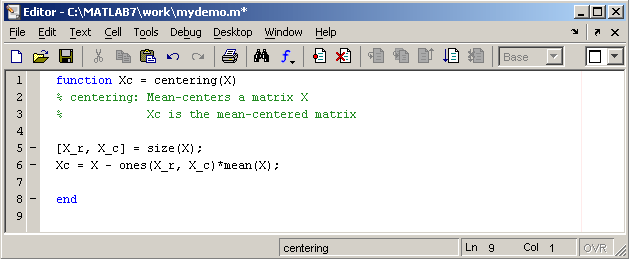
Слово function
в первой строке определяет, что данный
файл содержит файл-функцию. Первая
строка является заголовком функции, в
которой размещается имя функции и
списка входных и выходных аргументов. В
примере имя функции centering,
один входной аргумент X
и один выходной — Xc.
После заголовка следуют комментарии, а
затем — тело функции (оно в данном
примере состоит из двух строк), где и
вычисляется ее значение

Важно, что
вычисленное значение записывается в Xc.
Не забудьте поставить точку с запятой
для предотвращения вывода лишней
информации на экран. Теперь сохраните
файл в рабочем каталоге

Обратите
внимание, что выбор пункта Save или
Save as меню File
приводит к появлению диалогового окна
сохранения файла, в поле File name
которого уже содержится название centering.
Не изменяйте его, сохраните файл
функцию в файле с предложенным именем! 

Теперь созданную функцию
можно использовать так же, как и
встроенные sin,
cos и
другие. Вызов собственных функций
может осуществляться из файл-программы
и из другой файл-функции. Попробуйте
сами написать файл-функцию, которая
будет шкалировать матрицы, т.е. делить
каждый столбец на величину
среднеквадратичного отклонения по
этому столбцу. 

Можно написать файл-функции с
несколькими входными аргументами,
которые размещаются в списке через
запятую. Можно также создавать и
функции, возвращающие несколько
значений. Для этого выходные аргументы
добавляются через запятую в список
выходных аргументов, а сам список
заключается в квадратные скобки.
Хорошим примером является функция,
переводящая время, заданное в секундах,
в часы, минуты и секунды.

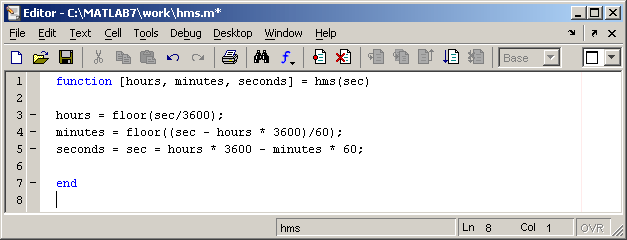
При вызове файл-функций с
несколькими выходными аргументами
результат следует записывать в вектор
соответствующей длины.

Полное описание

MATLAB включает в себя современные инструменты для анализа данных, разработки алгоритмов и создания различных моделей и приложений. Отличается от языков программирования C/C++, Java, Pascal, Fortran и прочих, более высокой скоростью решения типовых задач и получения результатов. Доступно HIL-тестирование созданного ПО в режиме реального времени.

Поддержка родного языка существенно упростит использование интерфейса. Софт предложит встроенные средства для работы с комплексными и аналитическими матрицами данных. Присутствуют встроенные функции линейной алгебры.

Зачастую программное обеспечение применяют в таких областях, как: разработка систем управления, автоматизация тестирования и измерений, моделирование объектов, вычислительная биология и так далее. Имеются удобные опции подсветки кода и подсказок для начинающих. МАТЛАБ станет незаменимым помощником в области технических вычислений и инженерных расчетов.

Меню состоит из нескольких окон, основные из которых:

1. Command Window — для ввода команд. После загрузки данного окна, курсор начнет моргать, соответственно можно приступать к работе.
2. Workspase — рабочее пространство. Здесь можно просматривать, редактировать и удалять объекты в памяти.
3. Current Folder — просмотр файловой структуры и выбор каталогов.
4. Command History отвечает за отображение списка использованных команд и их повторный вызов.

Вы сможете в любой момент закрыть одно или несколько окон, восстанавливать их, а также вручную настраивать размеры по собственному усмотрению.

Обратите внимание на рекомендуемые системные требования:

• ОЗУ: 2 Гб и выше;
• Видеокарта с поддержкой OpenGL 3.3;
• Свободное место на жестком диске: от 10 Гб;
• Процессор с тактовой частотой 2,2 ГГц и выше.

Creation

Description

creates a continuous-time transfer function model, setting the
and
properties. For instance, consider a continuous-time SISO dynamic system
represented by the transfer function ,
the input arguments and
are the coefficients of
and ,
respectively.

creates a discrete-time transfer function model, setting the
, , and
properties. For instance, consider a
discrete-time SISO dynamic system represented by the transfer function
, the input arguments
and are
the coefficients of and ,
respectively. To leave the sample time unspecified, set
input argument to .

creates a transfer function model with properties inherited from the dynamic
system model , including the sample time.

creates a transfer function model that represents the static gain,
.

sets properties of the transfer function model using one or more
pair arguments for any of the previous
input-argument combinations.

converts the dynamic system model to a transfer
function model.

converts the specified of
to transfer function form. Use this syntax
only when is an identified linear time-invariant
(LTI) model.

creates special variable
that you can use in a rational expression to create
a continuous-time transfer function model. Using a rational expression can
sometimes be easier and more intuitive than specifying polynomial
coefficients.

creates special
variable that you can use in a rational expression to
create a discrete-time transfer function model. To leave the sample time
unspecified, set input argument to
.

— Numerator coefficients of the transfer functionrow vector | -by- cell array of row
vectors

Numerator coefficients of the transfer function, specified as:

• A row vector of polynomial coefficients.

• An -by- cell array
  of row vectors to specify a MIMO transfer function, where
  is the number of outputs, and
  is the number of inputs.

When you create the transfer function, specify the numerator
coefficients in order of descending power. For instance, if the transfer
function numerator is , then specify
as . For a
discrete-time transfer function with numerator ,
set to .

Also a property of the object. For more
information, see .

— Denominator coefficients of the transfer functionrow vector | -by- cell array of row
vectors

Denominator coefficients, specified as:

• A row vector of polynomial coefficients.

• An -by- cell array
  of row vectors to specify a MIMO transfer function, where
  is the number of outputs and
  is the number of inputs.

When you create the transfer function, specify the denominator
coefficients in order of descending power. For instance, if the transfer
function denominator is , then specify
as . For
a discrete-time transfer function with denominator
, set to
.

Also a property of the object. For more
information, see .

— Dynamic systemdynamic system model | model array

Dynamic system, specified as a SISO or MIMO dynamic
system model or array of dynamic system models. Dynamic
systems that you can use include:

• Continuous-time or discrete-time numeric LTI models, such as
  , , , or

  models.

• Generalized or uncertain LTI models such as or
  (Robust Control Toolbox) models.
  (Using uncertain models requires Robust Control Toolbox software.)

  The resulting transfer function assumes

  • current values of the tunable components for tunable
    control design blocks.

  • nominal model values for uncertain control design
    blocks.

• Identified LTI models, such as (System Identification Toolbox), (System Identification Toolbox), (System Identification Toolbox),
  (System Identification Toolbox), and
  (System Identification Toolbox) models.
  To select the component of the identified model to convert,
  specify . If you do not specify
  ,
  converts the measured component of the identified model by
  default. (Using identified models
  requires System Identification Toolbox software.)

— Static gainscalar | matrix

Static gain, specified as a scalar or matrix. Static gain or steady
state gain of a system represents the ratio of the output to the input
under steady state condition.

— Component of identified model (default) | |

Component of identified model to convert, specified as one of the
following:

• — Convert the measured component
  of .

• — Convert the noise component of

• — Convert both the measured and
  noise components of .

only applies when
is an identified LTI model.

For more information on identified LTI models and their measured and
noise components, see .

Creation

Description

creates a continuous-time state-space model object of the following form:

x˙=Ax+Buy=Cx+Du

For instance, consider a plant with states,
outputs, and inputs. The state-space
matrices are:

• is an -by- real-
  or complex-valued matrix.

• is an -by- real-
  or complex-valued matrix.

• is an -by- real-
  or complex-valued matrix.

• is an -by- real-
  or complex-valued matrix.

creates the discrete-time state-space model object of the following form with the sample
time (in seconds):

xn+1=Axn+Bunyn=Cxn+Dun

To leave the sample time unspecified, set to
.

creates a state-space model with properties such as input and output names, internal
delays and sample time values inherited from the model .

creates a
state-space model that represents the static gain, . The output
state-space model is equivalent to .

sets properties of the state-space model using one or more
pair arguments for any of the previous input-argument
combinations.

converts the dynamic system model to a state-space model. If
contains tunable or uncertain elements,
uses the current or nominal values for those elements
respectively.

converts to object form the measured component, the noise
component or both of specified of an identified linear
time-invariant (LTI) model . Use this syntax only when
is an identified (LTI) model such as an (System Identification Toolbox), (System Identification Toolbox), (System Identification Toolbox), (System Identification Toolbox) or (System Identification Toolbox) object.

returns the minimal state-space realization with no uncontrollable or unobservable
states. This realization is equivalent to where
matrix has the smallest possible dimension.

Conversion to state-space form is not uniquely defined in the SISO case. It is also
not guaranteed to produce a minimal realization in the MIMO case. For more information,
see .

returns an explicit state-space realization (E = I) of the dynamic
system state-space model . returns an
error if is improper. For more information on explicit
state-space realization, see State-Space Models.

— Input-to-state matrix-by- matrix

Input-to-state matrix, specified as an
-by- matrix where,
is the number of states and is the number of inputs. This input
sets the value of property .

— State-to-output matrix-by- matrix

State-to-output matrix, specified as an
-by- matrix where,
is the number of states and is the number of outputs. This input
sets the value of property .

— Feedthrough matrix-by- matrix

Feedthrough matrix, specified as an -by-
matrix where, is the number of outputs and
is the number of inputs. This input sets the value of property .

— Dynamic system to convert to state-space formdynamic system model | model array

Dynamic system to convert to state-space form, specified as a SISO or MIMO dynamic system model or array of dynamic system
models. Dynamic systems that you can convert include:

• Continuous-time or discrete-time numeric LTI models, such as , , , or
  models.

• Generalized or uncertain LTI models such as or (Robust Control Toolbox) models. (Using uncertain models
  requires Robust Control Toolbox software.)

  The resulting state-space model assumes

  • current values of the tunable components for tunable control design
    blocks.

  • nominal model values for uncertain control design blocks.

• Identified LTI models, such as (System Identification Toolbox), (System Identification Toolbox), (System Identification Toolbox), (System Identification Toolbox), and (System Identification Toolbox) models. To select the
  component of the identified model to convert, specify
  . If you do not specify
  , converts the measured
  component of the identified model by default. (Using identified models requires System Identification Toolbox software.)

— Component of identified model (default) | |

Component of identified model to convert, specified as one of the
following:

• — Convert the measured component of
  .

• — Convert the noise component of

• — Convert both the measured and noise
  components of .

only applies when is an
identified LTI model.

For more information on identified LTI models and their measured and noise
components, see .

4.1. М-файлы

Работа из командной строки MatLab
затрудняется, если требуется вводить
много команд и часто их изменять.
Ведение дневника при помощи команды diary
и сохранение рабочей среды
незначительно облегчают работу. Самым
удобным способом выполнения групп
команд MatLab является использование М-файлов,
в которых можно набирать команды,
выполнять их все сразу или частями,
сохранять в файле и использовать в
дальнейшем. Для работы с М-файлами
предназначен редактор М-файлов. С его
помощью можно создавать собственные
функции и вызывать их, в том числе и из
командного окна. 

Раскройте меню File
основного окна MatLab и в пункте New
выберите подпункт M-file.
Новый файл открывается в окне редактора
M-файлов, которое изображено на рисунке.

М-файлы в MatLab бывают двух типов:
файл-программы (Script M-Files),
содержащие последовательность команд,
и файл-функции, (Function M-Files), в которых
описываются функции, определяемые
пользователем. 

3.2. Обмен данными между MatLab и Excel

Запустите Excel, проверьте, что
проделаны все необходимые настройки
так, как описано в предыдущем разделе (MatLab
должен быть закрыт). Введите в ячейки с
A1 по C3 матрицу, для отделения
десятичных знаков используйте точку в
соответствии с требованиями Excel. 

Выделите на листе данные
ячейки и нажмите кнопку putmatrix,
появляется окно Excel с предупреждением о
том, что MatLab не запущен. Нажмите OK,
дождитесь открытия MatLab. 

Появляется диалоговое окно Excel
со строкой ввода, предназначенной для
определения имени переменной рабочей
среды MatLab, в которую следует
экспортировать данные из выделенных
ячеек Excel. Введите к примеру, М и
закройте окно при помощи кнопки OK.
Перейдите к командному окну MatLab и
убедитесь, что в рабочей среде
создалась переменная М,
содержащая массив три на три:

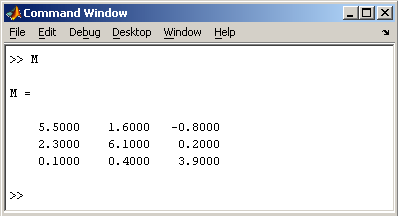
Проделайте некоторые операции
в MatLab с матрицей М, например,
обратите ее. 

Вызов inv
для обращения матрицы, как и любой
другой команды MatLab можно осуществить
прямо из Excel. Нажатие на кнопку evalstring,
расположенную на панели Excel Link,
приводит к появлению диалогового окна,
в строке ввода которого следует
набрать команду MatLab 

IM=inv(M). 

Результат аналогичен
полученному при выполнении команды в
среде MatLab. 

Вернитесь в Excel, сделайте
текущей ячейку A5 и нажмите кнопку
getmatrix.
Появляется диалоговое окно со строкой
ввода, в которой требуется ввести имя
переменной, импортируемой в Excel. В
данном случае такой переменной
является IM. Нажмите OK, в ячейки с
A5 по A7 введены элементы обратной
матрицы. 

Итак, для экспорта
матрицы в MatLab следует выделить
подходящие ячейки листа Excel, а для
импорта достаточно указать одну ячейку,
которая будет являться верхним левым
элементом импортируемого массива.
Остальные элементы запишутся в ячейки
листа согласно размерам массива,
переписывая содержащиеся в них данные,
поэтому следует соблюдать осторожность
при импорте массивов.

Вышеописанный подход является
самым простым способом обмена
информацией между приложениями —
исходные данные содержатся в Excel, затем
экспортируются в MatLab, обрабатываются
там некоторым образом и результат
импортируется в Excel. Пользователь
переносит данные при помощи кнопок
панели инструментов Excel Link.
Информация может быть представлена в
виде матрицы, т.е. прямоугольной
области рабочего листа. Ячейки,
расположенные в строку или столбец,
экспортируются, соответственно, в
векторы-строки и векторы-столбцы MatLab.
Аналогично происходит и импорт векторов-строк
и векторов-столбцов в Excel.

3.1. Конфигурирование Excel

Перед тем как настраивать Excel
на совместную работу с MatLab, следует
убедиться, что Excel Link входит в
установленную версию MatLab. В
подкаталоге exclink основного
каталога MatLab или подкаталога toolbox
должен находиться файл с надстройкой excllink.xla.
Запустите Excel и в меню Tools
выберите пункт Add-ins.
Откроется диалоговое окно, содержащее
информацию о доступных в данный момент
надстройках. Используя кнопку Browse,
укажите путь к файлу excllink.xla. В
списке надстроек диалогового окна
появится строка Excel Link 2.0 for use
with MatLab с установленным флагом.
Нажмите OK, требуемая
надстройка добавлена в Excel. 

Обратите внимание, что в Excel
теперь присутствует панель
инструментов Excel Link,
содержащая три кнопки: putmatrix,
getmatrix, evalstring.
Эти кнопки реализуют основные действия,
требуемые для осуществления
взаимосвязи между Excel и MatLab — обмен
матричными данными, и выполнение
команд MatLab из среды Excel. При повторных
запусках Excel надстройка excllink.xla
подключается автоматически. . Согласованная работа Excel и MatLab
требует еще нескольких установок,
которые приняты в Excel по умолчанию (но
могут быть изменены)

В меню Tools перейдите к пункту
Options,
открывается диалоговое окно Options.
Выберите вкладку General и
убедитесь, что флаг R1C1 reference style
выключен, т.е. ячейки нумеруются A1,
A2 и т.д.
На вкладке Edit должен
быть установлен флаг Move selection
after Enter.

Согласованная работа Excel и MatLab
требует еще нескольких установок,
которые приняты в Excel по умолчанию (но
могут быть изменены). В меню Tools перейдите к пункту
Options,
открывается диалоговое окно Options.
Выберите вкладку General и
убедитесь, что флаг R1C1 reference style
выключен, т.е. ячейки нумеруются A1,
A2 и т.д.
На вкладке Edit должен
быть установлен флаг Move selection
after Enter.

Description

performs
a logical AND of arrays and and
returns an array containing elements set to either logical 1 ()
or logical 0 (). An element of the output
array is set to logical 1 () if both and contain
a nonzero element at that same array location. Otherwise, the array
element is set to 0.

For bit-wise logical AND operations, see .

is
an alternate way to execute , but is rarely
used. It enables operator overloading for classes.

Examples

Locate Nonzero Values

Open Live Script

Find the logical AND of two matrices. The result contains logical () only where both matrices contain nonzero values.

A = 

A = 3×3

     5     7     0
     0     2     9
     5     0     0

B = 

B = 3×3

     6     6     0
     1     3     5
    -1     0     0

A & B

ans = 3x3 logical array

   1   1   0
   0   1   1
   1   0   0

Truth Table for Logical AND

Open Live Script

Create a truth table for .

A = 

A = 1x2 logical array

   1   0

B = 

B = 2x1 logical array

   1
   0

C = A&B

C = 2x2 logical array

   1   0
   0   0

Input Arguments

, — Operandsscalars | vectors | matrices | multidimensional arrays

Operands, specified as scalars, vectors, matrices, or multidimensional
arrays. Inputs and must either be
the same size or have sizes that are compatible (for example,
is an -by-
matrix and is a scalar or
-by- row vector). For more
information, see Compatible Array Sizes for Basic Operations.

Data Types: | | | | | | | | | |

Tips

• You can chain together several logical operations,
  for example, .

• The symbols and perform
  different operations in MATLAB. The element-wise AND operator described here is
  . The short-circuit AND operator is
  .

• When you use the element-wise and
  operators in the context of an or
  loop expression (and only in that context), they
  use short-circuiting to evaluate expressions. Otherwise, you must specify
  or to opt-in to
  short-circuiting behavior. See for more information.

Compatibility Considerations

Implicit expansion change affects arguments for operators

Behavior changed in R2016b

Starting in R2016b with the addition of implicit expansion, some combinations of arguments for basic operations that previously returned errors now produce results. For example, you previously could not add a row and a column vector, but those operands are now valid for addition. In other words, an expression like previously returned a size mismatch error, but now it executes.

If your code uses element-wise operators and relies on the errors that MATLAB previously returned for mismatched sizes, particularly within a / block, then your code might no longer catch those errors.

For more information on the required input sizes for basic array operations, see Compatible Array Sizes for Basic Operations.

Extended Capabilities

C/C++ Code GenerationGenerate C and C++ code using MATLAB Coder.

Thread-Based EnvironmentRun code in the background using MATLAB or accelerate code with Parallel Computing Toolbox .

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

| | | | |

1.6. Система помощи

Окно справки MatLab появляется
после выбора опции Help Window в
меню Help или нажатием
кнопки вопроса на панели инструментов.
Эта же операция может быть выполнена при
наборе команды helpwin.
Для вывода окна справки по отдельным
разделам, наберите helpwin
topic. Окно справки предоставляет
Вам такую же информацию, как и команда help,
но оконный интерфейс обеспечивает более
удобную связь с другими разделами
справки. Используя адрес Web-страницы
фирмы Math Works, вы
можете выйти на сервер фирмы и получить
самую последнюю информацию по
интересующим вас вопросам. Вы можете
ознакомиться с новыми программными
продуктами  или найти ответ на
возникшие проблемы на странице технической
поддержки.

Возможности MATLAB

• Разработка современных алгоритмов;
• Наличие средств интеграции с C/C++;
• Поддерживает функцию наследование кода;
• Позволяет проводить матричные вычисления;
• Возможность применения в разнообразных сферах;
• Встроенная система обработки сигналов и изображений;
• Создание внешних интерфейсов и независимых приложений;
• Включает в себя всю основу семейства продуктов MathWorks;
• Финансовое моделирование, проектирование коммуникационных систем;
• Последняя версия программы MATLAB r2017b совместима с ОС Windows 10 (64 bit);
• Значительно упрощает процесс решения широкого спектра задач на фоне других языков.

Преимущества

• Компиляция MEX-файлов;
• Автоматическая генерация кода;
• Встроенные математические функции;
• Присутствует поддержка 2-D и 3-D элементов;
• Гибкость в плане разработки новых алгоритмов;
• Наличие удобного пользовательского интерфейса;
• Доступно использование сложных структур данных;
• Ручная настройка размера окон и панелей с инструментами;
• Поддержка статистической типизации и модульной структуры;
• Совместимость с любыми процессорами Intel или AMD (x86, x64);
• Регулярные обновления софта от официального сайта компании MathWorks;
• Высокая популярность среди прикладных программ в области технических расчетов.

Недостатки

2.5. Матричные вычисления

MatLab содержит множество
различных функций для работы с
матрицами. Так, например,
транспонирование матрицы производится
при помощи апострофа ‘

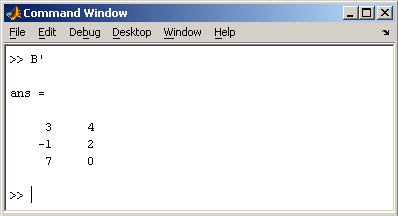
Нахождение обратной матрицы
проводится с помощью функции inv
для квадратных матриц

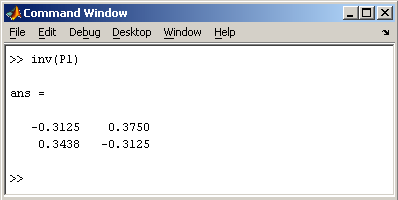
можно найти с помощью
функции pinv. 

Более
подробно про обработку матричных данных
можно узнать, если вывести список всех
встроенных функций обработки данных
командой help
datafun, а затем посмотреть
информацию о нужной функции, например help
max.

3. Интегрирование MatLab и Excel

Интегрирование MatLab и Excel
позволяет пользователю Excel обращаться
к многочисленным функциям MatLab для
обработки данных, различных вычислений
и визуализации результата. Надстройка excllink.xla
реализует данное расширение
возможностей Excel. Для связи MatLab и Excel
определены специальные функции.

4.2. Файл-программа

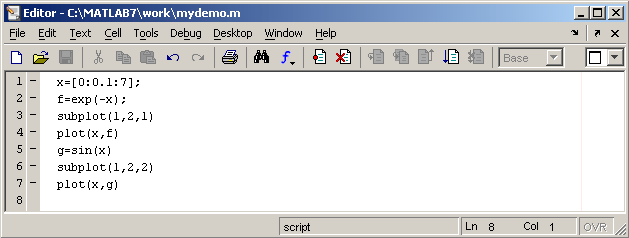
Наберите в редакторе команды,
приводящие к построению двух графиков
на одном графическом окне

Сохраните теперь файл с именем
mydemo.m в подкаталоге work
основного каталога MatLab, выбрав пункт Save
as меню File редактора. Для запуска на выполнение
всех команд, содержащихся в файле,
следует выбрать пункт Run в меню
Debug. На экране
появится графическое окно Figure 1,
содержащее графики функций. 

Команды файл-программы
осуществляют вывод в командное окно.
Для подавления вывода следует
завершать команды точкой с запятой.
Если при наборе сделана ошибка и MatLab не
может распознать команду, то
происходит выполнение команд до
неправильно введенной, после чего
выводится сообщение об ошибки в
командное окно. 

Очень удобной возможностью,
предоставляемой редактором М-файлов,
является выполнение части команд.
Закройте графическое окно Figure 1.
Выделите при помощи мыши, удерживая
левую кнопку, или клавишами со
стрелками при нажатой клавише Shift,
первые четыре команды и выполните их из
пункта Text

Обратите
внимание, что в графическое окно
вывелся только один график,
соответствующий выполненным: командам.
Запомните, что для выполнения части
команд их следует выделить и нажать
клавишу F9

Отдельные блоки М-файла можно
снабжать комментариями, которые
пропускаются при выполнении, но удобны
при работе с М-файлом. Комментарии
начинаются со знака процента и
автоматически выделяются зеленым
цветом, например:

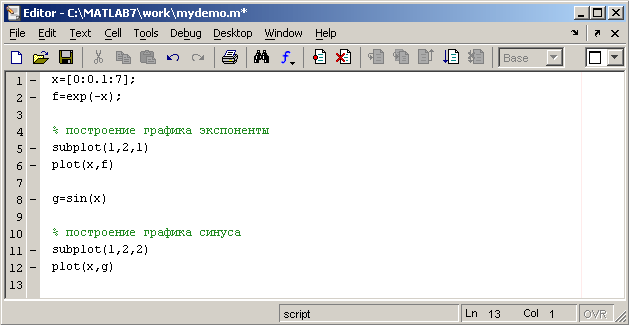
Открытие существующего М-файла
производится при помощи пункта Open меню
File рабочей среды,
либо редактора М-файлов.

1.5. Журнал

В MatLab имеется возможность
записывать исполняемые команды и
результаты в текстовый файл (вести
журнал работы), который потом можно
прочитать или распечатать из
текстового редактора. Для начала
ведения журнала служит команда diary.
В качестве аргумента команды diary
следует задать имя файла, в котором
будет храниться журнал работы.
Набираемые далее команды и результаты
их исполнения будут записываться я в
этот файл, например последовательность
команд

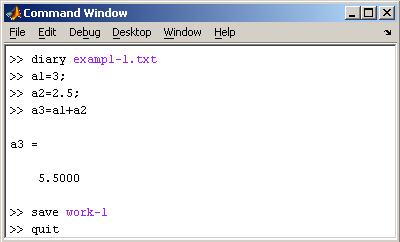
производит следующие действия: 

1. открывает
   журнал в файле exampl-1.txt; 

2. производит
   вычисления; 

3. сохраняет все
   переменные в MAT файле work-1.mat; 

4. сохраняет
   журнал в файле exampl-1.txt в
   подкаталоге work корневого
   каталога MatLab и закрывает MatLab; 

Посмотрите
содержимое файла exampl-1.txt в каком-нибудь
текстовом редакторе. В файле окажется
следующий текст: