Gnu octave version 4.2
Содержание:
- Ввод команд[править]
- Notable features[edit]
- How do I change color/line definition in gnuplot postscript?[edit]
- Installing Octave
- Простые примеры
- Эквивалентность
- Справка и документация[править]
- Соглашенияправить
- Entering commands[edit| edit source]
- Примечательные особенности
- Octave-Forge
- MATLAB compatibility[edit]
- Plotting[edit| edit source]
- Documentation
- Октава, язык
- История развития
- [править] Формат вывода значений
Ввод команд[править]
Последняя строка снизу является приглашением командной строки Octave и, так же как и командная строка в Linux, это место где вы вводите команды Octave. Чтобы выполнить простейшие арифметические операции, используйте + (сложение), — (вычитание), * (умножение), / (деление) и ^ (возведение в степень).
Также доступно много математических функций, имеющих предсказуемые имена (во многом схожие с аналогичными в других языках программирования).
Например:
- Тригонометрические функции: , ,
- Обратные тригонометрические функции: , ,
- Натуральный и десятичный логарифмы: ,
- Экспонента:
- Модуль числа:
Также определены различные константы: pi, e, мнимая единица (i или j), inf (бесконечность), NaN (Неопределенность. Результат неопределенных операций, например inf/inf).
Вот несколько примеров операций и соответствующих им команд Octave.
| 2+3{\displaystyle 2+3} |
octave:1> 2 + 3 ans = 5 |
| log10100log1010{\displaystyle {\frac {\log _{10}100}{\log _{10}10}}} |
octave:2> log10(100)/log10(10) ans = 2 |
| ⌊1+tan1.21.2⌋{\displaystyle \left\lfloor {\frac {1+\tan 1.2}{1.2}}\right\rfloor } |
octave:3> floor((1+tan(1.2)) / 1.2) ans = 2 |
| 32+42{\displaystyle {\sqrt {3^{2}+4^{2}}}} |
octave:4> sqrt(3^2 + 4^2) ans = 5 |
| ei⋅π{\displaystyle e^{i\cdot \pi }} |
octave:5> e^(i*pi) ans = -1.0000e+00 + 1.2246e-16i octave:6> # Comment: From Euler's famous formula octave:6> # extremely close to the correct value of -1 |
Несколько вещей, на которые стоит обратить внимание:
- В Octave требуются круглые скобки вокруг аргументов у функции (так, например log(10) — нормально, а вот (log 10) неверно).
- Любые пробелы до или после арифметических операций не являются обязательными, но допускаются
- Не все функции в Octave имеют очевидные имена (например, sqrt — извлечение корня). Не паникуйте. Вы узнаете о них по ходу обучения.
Notable features[edit]
Command and variable name completionedit
Typing a TAB character on the command line causes Octave to attempt to complete variable, function, and file names (similar to Bash’s tab completion). Octave uses the text before the cursor as the initial portion of the name to complete.
Command historyedit
When running interactively, Octave saves the commands typed in an internal buffer so that they can be recalled and edited.
Data structuresedit
Octave includes a limited amount of support for organizing data in structures. In this example, we see a structure «x» with elements «a», «b», and «c», (an integer, an array, and a string, respectively):
octave1> x.a = 1; x.b = 1, 2; 3, 4]; x.c = "string"; octave2> x.a ans = 1 octave3> x.b ans = 1 2 3 4 octave4> x.c ans = string octave5> x x = { a = 1 b = 1 2 3 4 c = string }
Short-circuit Boolean operatorsedit
Octave’s and logical operators are evaluated in a short-circuit fashion (like the corresponding operators in the C language), in contrast to the element-by-element operators and .
Increment and decrement operatorsedit
Octave includes the C-like increment and decrement operators and in both their prefix and postfix forms. Octave also does augmented assignment, e.g. .
Unwind-protectedit
unwind_protect body unwind_protect_cleanup cleanup end_unwind_protect
As a general rule, GNU Octave recognizes as termination of a given either the keyword (which is compatible with the MATLAB language) or a more specific keyword . As a consequence, an block can be terminated either with the keyword as in the example, or with the more portable keyword .
The cleanup part of the block is always executed. In case an exception is raised by the body part, cleanup is executed immediately before propagating the exception outside the block .
GNU Octave also supports another form of exception handling (compatible with the MATLAB language):
try body catch exception_handling end
This latter form differs from an block in two ways. First, exception_handling is only executed when an exception is raised by body. Second, after the execution of exception_handling the exception is not propagated outside the block (unless a statement is explicitly inserted within the exception_handling code).
Variable-length argument listsedit
Octave has a mechanism for handling functions that take an unspecified number of arguments without explicit upper limit. To specify a list of zero or more arguments, use the special argument as the last (or only) argument in the list.
functions=plus (varargin) if (nargin==) s = ; else s = varargin{1} + plus (varargin{2nargin}); end end
Variable-length return listsedit
A function can be set up to return any number of values by using the special return value . For example:
functionvarargout=multiassign (data) for k=1nargout varargout{k} = data(:,k); end end
C++ integrationedit
It is also possible to execute Octave code directly in a C++ program. For example, here is a code snippet for calling :
#include <octave/oct.h> ... ColumnVector NumRands(2); NumRands() = 10; NumRands(1) = 1; octave_value_list f_arg, f_ret; f_arg() = octave_value(NumRands); f_ret = feval("rand", f_arg, 1); Matrix unis(f_ret().matrix_value());
C and C++ code can be integrated into GNU Octave by creating oct files, or using the MATLAB compatible MEX files.
How do I change color/line definition in gnuplot postscript?[edit]
Here is a awk script to get a rainbow color map
#!/bin/awk -f
BEGIN {
split("0 4 6 7 5 3 1 2 8", rainbow, " ");
split("7 3 1 0 2 4 6 5 8", invraim, " ");
}
$1 ~ /\/LT/ {
n = substr($1, 4, 1);
if (n == 0)
lt = "{ PL [] 0.9 0.1 0.1 DL } def";
else if (n == 1)
lt = "{ PL 0.1 .75 0.1 DL } def";
else if (n == 2)
lt = "{ PL 0.1 0.1 0.9 DL } def";
else if (n == 3)
lt = "{ PL 0.9 0 0.8 DL } def";
else if (n == 4)
lt = "{ PL 0.1 0.8 0.8 DL } def";
else if (n == 5)
lt = "{ PL 0.9 0.8 0.2 DL } def";
else if (n == 6)
lt = "{ PL 0.5 0.3 0.1 DL } def";
else if (n == 7)
lt = "{ PL 1 0.4 0 DL } def";
else if (n == 8)
lt = "{ PL 0.5 0.5 0.5 DL } def";
$0 = sprintf("/LT%d %s", rainbow, lt);
##$0 = sprintf("/LT%x %s", invraim, lt);
##$0 = sprintf("/LT%x %s", n, lt);
}
{ print; }
Installing Octave
Octave is availabe for most platforms (Windows, Mac OS X, Linux). I will be showing you instructions on how to install Octave on a Debian-based Linux machine, so if you are not working on Linux, you may have to Google how to set it up.
As root, type: in your console.
After a few short lines of text from the console, with any luck Octave should be installed. To see if it is installed, type: in the console, and the octave interpreter (program) should be running and you should see something similar to the following below:
At the prompt, you can type then press enter, or do CTRL + D to quit the interpreter. Great! We are ready to move on.
Простые примеры
Рассмотрим несколько простых примеров, чтобы максимально быстро войти в курс дела и понять как все тут работает. Взято с документации.
Элементарные вычисления
Octave поддерживает следующие арифметические операции + - * , возведение в степень ^, натуральные логарифмы/показатели (log, exp), тригонометрические функции (sin, cos, …). Кроме этого, Octave может работать как с вещественными числами, так и с комплексными (i, j). Также предопределены некоторые математические константы, например, число pi и основание натурального логарифма e.
Попробуем для начала проверить тождество Эйлера.
Вводим в командное окно следующее выражение:
>> exp(i*pi)
Ответ должен быть равен -1, я у себя получил следующее:
ans = -1.0000e+00 + 1.2246e-16i
Создание матриц
Векторы и матрицы базовые строительные блоки числового анализа. Для создания матрицы и сохранения ее в переменную для последующего использования нужно ввести следующую команду:
>> A =
И получим ответ:
A =
1 1 2
3 5 8
13 21 34
Если ввести команду, поставив в конце точку с запятой, то Octave не будет выводить матрицу на экран, например, создадим матрицу на 3 строки и 2 столбца со случайными числами:
>> B = rand (3, 2);
Теперь для того, чтобы получить вывод данной матрицы на экран, достаточно ввести в командное окно имя переменной, в которой она сохранена:
>> B
Арифметика матриц
Умножение матрицы на скаляр:
>> 2 * A
Перемножение двух матриц:
>> A * B
Умножение транспонированной матрицы на саму себя:
>> A' * A
Решение систем линейных уравнений
Разберем на примере следующего уравнения
Распишем матрицы коэффициентов и свободных членов для этой системы уравнений
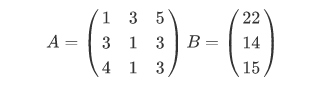
Теперь набираем обе получившиеся матрицы в Octave и решаем систему методом наименьших квадратов с помощью, так называемого оператора левого деления \
>> A = ; >> B = ; >> A\B ans = 1.0000 2.0000 3.0000
Решение нелинейных дифференциальных уравнений
Octave может проинтегрировать уравнения следующего вида
Пробуем ввести функцию в Octave, сделать это несложно, гораздо сложнее понять, что ты только что сделал) Я уже давно забыл всю теорию вышмата, так что просто повторил пример и это работает, позже уже буду разбираться как.
>> function xdot = f (x, t)
r = 0.25;
k = 1.4;
a = 1.5;
b = 0.16;
c = 0.9;
d = 0.8;
xdot(1) = r*x(1)*(1 - x(1)/k) - a*x(1)*x(2)/(1 + b*x(1));
xdot(2) = c*a*x(1)*x(2)/(1 + b*x(1)) - d*x(2);
endfunction
>> x0 = ;
>> t = linspace (0, 50, 200)';
>> x = lsode ("f", x0, t);
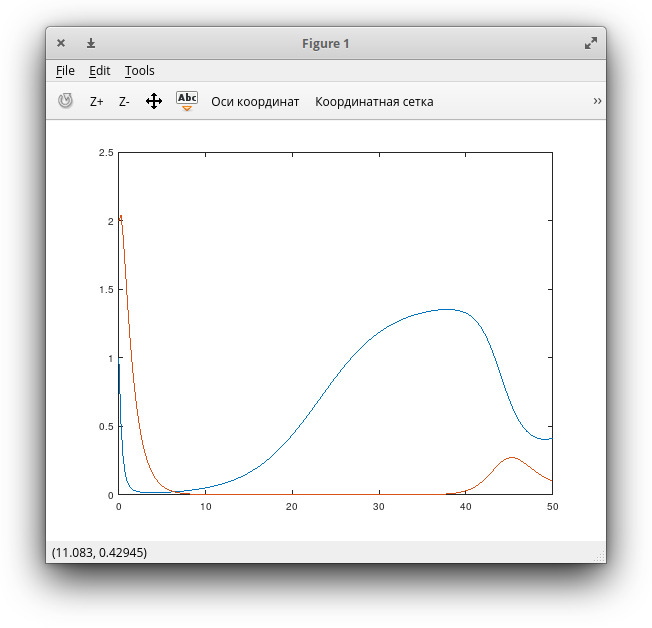
Последняя команда производит интегрирование и если ее выполнить без ; в конце, то можно будет увидеть много цифр рассчитанной функциональной зависимости.

Графический вывод
Чтобы получить график, полученного в прошлом примере решения достаточно ввести команду:
>> plot (t, x)
Octave тут же создаст новое окно с вот таким вот красивым графиком, который к тому же можно сохранить скажем в pdf формат командой:
>> print -dpdf ~/foo.pdf
Пока на этом все, буду стараться использовать Octave в разработке и если у меня будет получаться, то я непременно напишу об этом в блоге. А пока подписывайтесь куда-нибудь (ВК, Твиттер), что-нибудь жмите, что-нибудь пишите (Телеграм). Всем пока!
Эквивалентность
Ваш браузер не поддерживает воспроизведение звука. Вы можете скачать аудиофайл .
Ваш браузер не поддерживает воспроизведение звука. Вы можете скачать аудиофайл .
Ваш браузер не поддерживает воспроизведение звука. Вы можете скачать аудиофайл .
Демонстрация октавной эквивалентности. Мелодия к « Мерцай, мерцай, звездочка » с параллельной гармонией . Мелодия параллельна тремя способами: (1) октавами ( согласными и эквивалентными); (2) в пятых (достаточно согласный, но не эквивалентный); и (3) в секундах (ни согласных, ни эквивалентных).
После унисона октава — самый простой интервал в музыке. Человеческое ухо имеет тенденцию слышать обе ноты как «одинаковые» из-за тесно связанных гармоник. Ноты разделены октавным «кольцом» вместе, что придает музыке приятный звук. Интервал настолько естественен для людей, что, когда мужчин и женщин просят петь в унисон, они обычно поют в октаве.
По этой причине нотам, разнесенным на октаву, в западной системе музыкальной нотации дается одно и то же название — имя ноты на октаву выше А также является А. Это называется октавной эквивалентностью , т.е. музыкально эквивалентны во многих отношениях, что приводит к соглашению, что « гаммы однозначно определяются путем указания интервалов в октаве». Концептуализация высоты звука как имеющей два измерения, высоту звука (абсолютная частота) и класс высоты звука (относительное положение в пределах октавы), по сути, включает октавную округлость. Таким образом, все C ♯ или все единицы (если C = 0) в любой октаве являются частью одного и того же класса высоты звука .
Эквивалентность октав является частью большинства продвинутых музыкальных культур, но далеко не универсальна в «примитивной» и ранней музыке . В языках, на которых написаны самые старые из сохранившихся письменных документов по настройке, шумерском и аккадском , нет известного слова, обозначающего «октаву». Однако считается, что набор клинописных табличек, которые в совокупности описывают настройку девятиструнного инструмента, считающегося вавилонской лирой , описывают настройки для семи струн с указаниями для настройки оставшихся двух струн на октаву из двух. из семи настроенных струн. Леон Крикмор недавно предположил, что «октава, возможно, не рассматривалась как отдельная единица, а скорее по аналогии с первым днем новой семидневной недели».
Обезьяны испытывают октавную эквивалентность, и ее биологическая основа, очевидно, является октавным картированием нейронов в слуховом таламусе мозга млекопитающих . Исследования также показали восприятие эквивалентности октав у крыс, человеческих младенцев и музыкантов, но не у скворцов, детей 4–9 лет или музыкантов.
Справка и документация[править]
Octave имеет обширную справочную информацию, доступ к которой можно получить из командной строки Octave.
Для получения справочной информации, вы должны знать имя команды, о которой требуется получить справку. Имя функции может быть не всегда очевидным, хороший способ — набрать для начала команду «help». Она покажет все операторы, зарезервированные слова, функции, встроенные переменные и функции файлов. Другой способ — выполнить поиск с помощью функции «lookfor». Эта функция описывается в разделе «Получение помощи».
После того, как вам станет известно имя функции, о которой вы хотите получить справку, введите его в качестве аргумента команды «help». Например:
helpplot
отобразит справку для функции «plot».
Для вывода на экран информации, которая не может полностью на нём поместиться, Octave использует пейджеры на подобие less и more. Нажатие «Enter» выводит следующую строку, «Пробел» — следующую страницу. Клавиша «q» закрывает пейджер.
Соглашенияправить
Этот раздел объясняет типографические соглашения, используемые в этом руководстве. Возможно вы захотите пропустить этот раздел и вернуться к нему позже.
Entering commands[edit| edit source]
The last line above is known as the Octave prompt and, much like the prompt in Linux, this is where you type Octave commands. To do simple arithmetic, use (addition), (subtraction),
(multiplication), (division), and (exponentiation).
Many mathematical functions are available and have obvious names (with many of those similar to other programming languages). For example, we have:
- trigonometric functions: , ,
- inverse trigonometric functions: , ,
- natural and base 10 logarithms: ,
- exponentiation:
- absolute value:
Various constants are also pre-defined: , (Euler’s number), and (the imaginary number sqrt(-1)), (Infinity), (Not a Number — resulting from undefined operations, such as .)
Here are some examples showing the input typed at the prompt and the output returned by Octave.
| 2+3{\displaystyle 2+3} | log10100log1010{\displaystyle {\frac {\log _{10}100}{\log _{10}10}}} | ⌊1+tan1.21.2⌋{\displaystyle \left\lfloor {\frac {1+\tan 1.2}{1.2}}\right\rfloor } | 32+42{\displaystyle {\sqrt {3^{2}+4^{2}}}} |
octave:1> 2 + 3 ans = 5 |
octave:2> log10(100)/log10(10) ans = 2 |
octave:3> floor((1+tan(1.2)) / 1.2) ans = 2 |
octave:4> sqrt(3^2 + 4^2) ans = 5 |
| ei⋅π{\displaystyle e^{i\cdot \pi }} |
octave:5> e^(i*pi) ans = -1.0000e+00 + 1.2246e-16i octave:6> # Comment: From Euler's famous formula octave:6> # extremely close to the correct value of -1 |
Some things to note:
- Octave requires parentheses around the input of a function (so, is fine, but () is not).
- Any spacing before and after arithmetic operators is optional, but allowed.
- Not all Octave functions have obvious names (e.g. above). Don’t panic for now. You will get to know them as we go along.
Примечательные особенности
Завершение имени команды и переменной
Ввод символа TAB в командной строке заставляет Octave пытаться завершить имена переменных, функций и файлов (аналогично Башс завершение табуляции). Octave использует текст перед курсором как начальную часть имени для завершения.
История команд
При работе в интерактивном режиме Octave сохраняет набранные команды во внутреннем буфере, чтобы их можно было вызывать и редактировать.
Структуры данных
Octave включает ограниченный объем поддержки для организации данных в структурах. В этом примере мы видим структуру «x» с элементами «a», «b» и «c» (целое число, массив и строка соответственно):
октава1> Икс.а = 1; Икс.б = 1, 2; 3, 4]; Икс.c = "строка";октава2> Икс.аответ = 1октава3> Икс.бответ = 1 2 3 4октава4> Икс.cответ = строкаоктава5> ИксИкс ={ а = 1 б = 1 2 3 4 c = строка}
Булевы операторы короткого замыкания
Октава » и ‘логичный операторы оцениваются в короткое замыкание мода (как и соответствующие операторы в C язык), в отличие от поэлементных операторов » и ».
Операторы увеличения и уменьшения
Octave включает C-подобный операторы увеличения и уменьшения » и »как в префиксной, так и в постфиксной форме. Octave также расширенное задание, например ».
Расслабься-защити
unwind_protect телоunwind_protect_cleanup уборкаend_unwind_protect
Как правило, GNU Octave распознает прекращение заданного »либо ключевое слово»(который совместим с языком MATLAB) или более конкретное ключевое слово». Как следствие,’блок может быть завершен ключевым словом»как в примере, или с более переносимым ключевым словом».
В уборка часть блока всегда выполняется. Если исключение вызвано тело часть, уборка выполняется непосредственно перед распространением исключения за пределы блока ».
GNU Octave также поддерживает другую форму обработки исключений (совместимую с языком MATLAB):
пытаться телоловить Обработка исключенийконец
Эта последняя форма отличается от »заблокировать двумя способами. Первый, Обработка исключений выполняется только тогда, когда исключение вызывается тело. Во-вторых, после казни Обработка исключений исключение не распространяется за пределы блока (если только »оператор явно вставлен в Обработка исключений код).
Списки аргументов переменной длины
Octave имеет механизм обработки функций, которые принимают неопределенное количество аргументов без явного верхнего предела. Чтобы указать список из нуля или более аргументов, используйте специальный аргумент как последний (или единственный) аргумент в списке.
функцияs =плюс (вараргин)если (наргин==) s = ; еще s = вараргин{1} + плюс (вараргин{2наргин}); конецконец
Списки возврата переменной длины
Функцию можно настроить так, чтобы она возвращала любое количество значений, используя специальное возвращаемое значение. . Например:
функциявараргут =многопользовательский (данные)для k=1Наргут вараргут{k} = данные(:,k); конецконец
Интеграция с C ++
Также возможно выполнить код Octave непосредственно в программе на C ++. Например, вот фрагмент кода для вызова :
#включают <octave/oct.h>...СтолбецВектор NumRands(2);NumRands() = 10;NumRands(1) = 1;octave_value_list f_arg, f_ret;f_arg() = octave_value(NumRands);f_ret = лихорадка("ранд", f_arg, 1);Матрица unis(f_ret().matrix_value());
Код C и C ++ может быть интегрирован в GNU Octave, создав файлы oct или используя совместимый с MATLAB Файлы MEX.
Octave-Forge
Packages can be installed or .
Using Octave’s installer
Packages can be managed using Octave’s installer. They are installed to ~/octave, or in a system directory with the -global option. To install a package:
octave:1> pkg install -forge packagename
Note: Some Octave’s packages, like , need the ArchLinux’s package in order to compile and install.
To uninstall a package:
octave:3> pkg uninstall packagename
Some packages get loaded automatically by Octave, for those which do not:
octave:4> pkg load packagename
or
octave:5> pkg load all
To see which packages have been loaded use , the packages with an asterisk are the ones that are already loaded.
A way to make sure that all packages gets loaded at Octave startup:
/usr/share/octave/site/m/startup/octaverc
## System-wide startup file for Octave. ## ## This file should contain any commands that should be executed each ## time Octave starts for every user at this site. pkg load all
MATLAB compatibility[edit]
Octave has been built with MATLAB compatibility in mind, and shares many features with MATLAB:
- Matrices as fundamental data type.
- Built-in support for complex numbers.
- Powerful built-in math functions and extensive function libraries.
- Extensibility in the form of user-defined functions.
Octave treats incompatibility with MATLAB as a bug; therefore, it could be considered a software clone, which does not infringe software copyright as per Lotus v. Borland court case.
MATLAB scripts from the MathWorks’ FileExchange repository in principle are compatible with Octave. However, while they are often provided and uploaded by users under an Octave compatible and proper open source BSD license, the FileExchange Terms of use prohibit any usage beside MathWorks’ proprietary MATLAB.
Syntax compatibilityedit
- Comment lines can be prefixed with the # character as well as the % character;
- Various C-based operators ++, —, +=, *=, /= are supported;
- Elements can be referenced without creating a new variable by cascaded indexing, e.g. (3);
- Strings can be defined with the double-quote » character as well as the single-quote ‘ character;
- When the variable type is single (a single-precision floating-point number), Octave calculates the «mean» in the single-domain (MATLAB in double-domain) which is faster but gives less accurate results;
- Blocks can also be terminated with more specific Control structure keywords, i.e., endif, endfor, endwhile, etc.;
- Functions can be defined within scripts and at the Octave prompt;
- Presence of a do-until loop (similar to do-while in C).
Function compatibilityedit
When an unimplemented function is called the following error message is shown:
octave1> guide warning the 'guide' function is not yet implemented in Octave Please read <http//www.octave.orgmissing.html> to learn how you can contribute missing functionality. error 'guide' undefined near line 1 column 1
Plotting[edit| edit source]
You are going to plot the following pictures using Octave:
| Figure 1 | Figure 2 |
| Figure 3 | Figure 4 |
Figure 1 contains a plot of sin x vs x and is generated with the following commands. While this is a simple example, it is meant to illustrate the basic functionality. We will see more elaborate examples later.
x = linspace(0, 2*pi, 100); y = sin(x); plot(x, y); figure;
The command that actually generates the plot is, of course, . Before executing this command, we need to set up the variables, x and y. The function simply takes two vectors of equal length as input, interprets the values in the first as x-coordinates and the second as y-coordinates and draws a line connecting these coordinates.
The first command above, , uses the function to make a vector of equally spaced intervals (sometimes also called «linearly spaced values»). The first value in the vector is 0, the final value is 2π and the vector contains 100 values. This vector is assigned to the variable named .
The second command computes the sin of each value in the vector variable, , and stores the resulting vector in the variable .
(As an aside: the name of a variable can be any sequence of letters, digits and underscores that does not start with a digit. There is no maximum length for variable names, and the case of alphabetical characters is important, i.e. and are two different variable names.)
Exerciseedit| edit source
Plot the function y=⌊x⌋{\displaystyle y=\lfloor x\rfloor } for x∈,15{\displaystyle x\in }. (This is Figure 2).
Note : The graph may appear slightly inaccurate if the length(3rd) parameter of linspace is not sufficiently large. See the next heading for more information.
More on commandsedit| edit source
The following commands and functions are useful for setting up variables for plotting 2D graphs.
linspace creates a vector of evenly (linearly) spaced values.
Usage: . The parameter is optional and specifies the number of values in the returned vector. If you leave out this parameter, the vector will contain 100 elements with as the first value and stop as the last.
plot plots a 2-dimensional graph.
Usage: where and are vectors of equal length.
figure creates a new plotting window.
This is useful for when you want to plot multiple graphs in separate windows rather than replacing your previous graph or plotting on the same axes.
hold on and hold off sets whether you want successive plots to be drawn together on the same axes or to replace the previous plot.
The ; at the end of a line suppress the display of the result. Try to remove it, and see !
Exampleedit| edit source
We are going to plot Figures 3 and 4. Figure 3 contains the 3 trigonometric functions
- cos2x{\displaystyle \cos 2x},
- sin4x{\displaystyle \sin 4x}, and
- 2sinx{\displaystyle 2\sin x}
on one set of axes. Figure 4 contains the sum of these 3 functions.
Firstly, we use to set up a vector of x-values.
octave:1> x = linspace(0, 2*pi);
Then, we compute the y-values of the 3 functions.
octave:2> a = cos(2*x); octave:3> b = sin(4*x); octave:4> c = 2*sin(x);
The following plots the first graph.
octave:5> figure; octave:6> plot(x, a); octave:7> hold on; octave:8> plot(x, b); octave:9> plot(x, c);
We use line 5 () to tell Octave that we want to plot on a new set of axes. It is good practice to use before plotting any new graph. This prevents you from accidentally replacing a previous plot with the new one.
Note that on line 7, is used to tell Octave that we don’t want to replace the first plot (from line 6) with subsequent ones. Octave will plot everything after on the same axes, until the command is issued.
The figure you see shows all three plotted functions in the same color. To let Octave assign different colors automatically plot all functions in one step.
octave:10> plot(x, a, x, b, x, c);
Finally, we plot the second graph.
octave:11> figure; octave:12> hold off; octave:13> plot(x, a+b+c);
Line 11 creates a new graph window and line 12 tells Octave that any subsequent plots should simply replace previous ones. Line 13 generates the plot of the sum of the 3 trigonometric functions.
A small note for mac users, if plot figure commands do not work first use this command:
> setenv («GNUTERM», «x11»)
Documentation
- Improve documentation for function (bug #60817).
- : Fix typo in “see also” section of docstring (bug #60842).
- , : Document that functions might return minimum norm solutions (bug #60839).
- Improve Differential Equations chapter and example for lsode (bug #57508).
- Clarify usage of “Depends” keyword in package file (bug #60053).
- Add note that wildcard patterns for are glob patterns (bug #60157).
- Change example for Delaunay triangulation to match the generating code (bug #60216).
- Document single precision issues with OpenGL graphics toolkits (bug #59418).
- Minor changes to documentation of single precision issues with OpenGL (bug #59418).
- Expand on documentation for command syntax (bug #60084).
- : Document that function only works on graphics objects in Octave 6.X (bug #60295).
- Explain how to write dual-purpose executable scripts and Octave functions (bug #60291).
- Update keyword docstrings (bug #60275).
- Use Texinfo commands to improve docstring rendering.
- , : Correct non-TeX definition of beta incomplete integral.
- Grammarcheck documentation ahead of 6.3 release.
- Spellcheck documentation ahead of 6.3 release.
Октава, язык
Программы Octave состоят из списка вызовов функций или сценария . Синтаксис основан на матрице и предоставляет различные функции для матричных операций. Он поддерживает различные структуры данных и позволяет объектно-ориентированное программирование .
Его синтаксис очень похож на MATLAB, и тщательное программирование скрипта позволит ему работать как в Octave, так и в MATLAB.
Поскольку Octave предоставляется под Стандартной общественной лицензией GNU , ее можно свободно изменять, копировать и использовать. Программа работает в Microsoft Windows и большинстве Unix и Unix-подобных операционных систем , включая Linux , Android и macOS .
История развития
| Время | Действие |
|---|---|
| 1988/1989 | 1-е обсуждение (книга и программное обеспечение) |
| Февраль 1992 г. | Начало разработки |
| Январь 1993 | Новости в Интернете (версия 0.60) |
| Февраль 1994 | Первая публикация (версии с 1.0.0 по 1.1.1) |
| Декабрь 1996 г. | 2-я публикация (версия 2.0.x) с портом Windows ( Cygwin ) |
| Март 1998 г. | Версия 2.1 |
| Ноябрь 2004 г. | Версия 2.9 (DEV версия 3.0) |
| Декабрь 2007 г. | Публикация версии 3.0 (Milestone) |
| Июнь 2009 г. | Публикация версии 3.2 (Milestone) |
| 8 февраля 2011 г. | Версия 3.4.0 (Milestone) |
| 22 февраля 2012 г. | Публикация Octave 3.6.1 (Milestone) |
| 31 декабря 2013 г. | Публикация Octave 3.8.0 (экспериментальный графический интерфейс) |
| 29 мая 2015 | Версия 4.0.0 (стабильный графический интерфейс и новый синтаксис для ООП ) |
| 14 ноября 2016 г. | Версия 4.2.0 (gnuplot 4.4+) |
| 30 апреля 2018 г. | Версия 4.4.0 (новая цель для GUI QT Toolkit, инструментарий FLTK не является устаревшим, и нет графика для его удаления — хотя больше не имеет приоритета) |
| 1 марта 2019 г. | Публикация Octave 5.1.0 (предпочтительно QT5, минимум Qt 4.8), поддержка hiDpi |
| 31 января 2020 г. | Публикация Octave 5.2.0 (предпочтительно QT5) |
| 26 ноября 2020 г. | Публикация Octave 6.1.0 (QT5 предпочтительно, Qt 4.x не рекомендуется для удаления в 7) |
| 20 февраля 2021 г. | Публикация Octave 6.2.0 (предпочтительно QT5), исправление ошибок, улучшенная поддержка синтаксиса Matlab |
[править] Формат вывода значений
Очевидно, что в разных случаях необходимо выводить результаты вычислений с различной точностью. Для этих целей служит команда format.
Синтаксис:
где <опция> может принимать одно из значений:
| bank | — 2 знака после запятой |
| short | — 5 знаков после запятой (используется по умолчанию) |
| short e или E | — то же, но в инженерном формате с соответствующей буквой |
| short g или G | — автоматический выбор между short и short е/Е |
| long | — 15 знаков после запятой |
| long e или E | — то же, но в инженерном формате с соответствующей буквой |
| long g или G | — автоматический выбор между long и long е/Е |
| bit | — представление числа в двоичной системе исчисления (в 32- или 64-битном представлении, смотря какая машина) |
| hex | — представление числа в шестнадцатеричной системе исчисления (в 32- или 64-битном представлении, смотря какая машина) |
| free | — свободный формат |
Пример использования:
> format bank # устанавливаем формат > 1/3 # для примера, получаем какое-либо дробное число ans = 0.33 > > format short e # устанавливаем новый формат > 1/3 ans = 3.3333e-001