Инженерное моделирование квазистатического электромагнитного поля в программе elcut для задач электроники

Введение

Более столетия назад инженеры, работающие с задачами электромагнитного поля, разделились на две слабо связанные культуры: низкочастотные поля большой мощности (электротехника) и высоко­частотные поля относительно малой мощности (электроника). Несмотря на то, что обе группы работают с решениями уравнений Максвелла, в каждом практическом случае эти уравнения решаются в разных приближениях и допущениях, специально подобранных для адекватного описания конкретного круга задач.

Традиционной средой обитания расчетчиков современной электронной техники является высокочастотная часть спектра электромагнитного поля, где господствуют волновые решения. В то же время в задачах электротехники уравнения Максвелла обычно записываются в допущениях, приводящих к уравнению диффузии, у которого волновые решения отсутствуют.

В данном обзоре предпринята попытка осмысления того, как программа ELCUT, использующая низко­частотное (квазистационарное) приближение уравнений электромагнитного поля, может быть использована в задачах проектирования электронной техники и где проходит граница ее применимости.

Возможно, вам также будет интересно

Современные радиоэлектронные системы содержат множество различных типов компонентов и узлов, для эффективного моделирования которых следует использовать подходящие численные методы. Так, например, простая высокочастотная система может включать фильтры, классически анализируемые частотными методами, или антенны, для расчета которых, как правило, используются вычислители во временной области, или корпус изделия, лучшим образом моделируемый с использованием метода матриц линий передач. Кроме того, параметры

В настоящее время все больше внимания уделяется проблемам негативного влияния на человека электромагнитных полей (ЭМП) и радиоизлучений. Электромагнитные поля — это особая форма существования материи, характеризующаяся совокупностью электрических и магнитных свойств. Электромагнитные поля окружают нас повсюду, но мы не можем их почувствовать и вообще заметить, поэтому мы не видим излучений милицейского радара и полей, наводимых

Несмотря на широкое обсуждение и наличие рекомендаций по проектированию конструкции преобразователей для обеспечения электромагнитной совместимости (EMC) компонентов, взаимодействие между различными функциональными группами в устройствах может привести к нежелательным побочным эффектам, проявляемым при проведении лабораторных тестов EMC. Даже при установке изделия в металлический корпус может случиться так, что уровень излучаемых помех превысит пороговое значение.

Совместимость с Windows 7

Начиная с версии 5.8, ELCUT полностью совместим с Windows 7. Заново переписанная программа установки теперь обеспечивает следующие возможности:

1. Полная совместимость с Windows 7, включая взаимодействие с режимом UAC (средство контроля пользовательских учетных записей).
2. Использование последней версии программного обеспечения SafeNet – драйвер ключа аппаратной защиты и сервер безопасности.
3. Корректная регистрация и удаление всех компонентов программы.
4. Администратор имеет возможность подготовить для своих пользователей специальную преднастроенную версию пакета установки ELCUT.

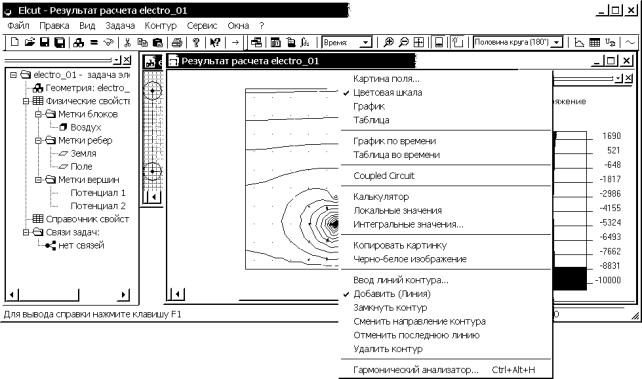
Рис. 4.27. Окно выбора отображаемых параметров поля

Для ввода контура строят
первую линию и от ее конца ведут следующую и т.д. пока контур не замкнется.
Иногда удобно использовать команду “Замкнуть” меню Контур или команду “Замкнуть
контур” из списка команд контекстного меню. Любой контур имеет направление
обхода, которое отражается стрелкой при каждой линии, ограничивающей его.

При создании линий можно
задавать тип их контура: прямая линия, четверть круга, половина круга, три
четверти круга, в соответствующей вкладке “Раствор дуги” на панели анализа
результатов.

Для редактирования созданных
линий и контуров, их удаления или смены направления обхода пользуются командами
меню Контур или вызывают правой кнопкой мыши контекстное меню и выбирают
соответствующую команду (рис. 4.28).

Для точного ввода начальных
и конечных координат линий или контуров следует вызвать окно “Добавление линий”
через меню Контур, где выбираем “Ввод линий…” или через контекстное меню,
выбрать команду “Ввод линий контура…”.

8.4. В качестве примера
построим график изменения потенциала при х
= 0 вдоль оси у. Для точного задания
начала и конца линии, щелкнув правой кнопкой мыши в окне результатов расчета,
из контекстного меню выбираем команду “Ввод линий контура…”. Первая точка имеет
координаты (0, 0), нажимаем левой кнопкой мыши на пункт “Начальная точка”.
Пункт “Начальная точка” сменяется пунктом “Добавить линию”. Вводим с клавиатуры
координаты второй точки (0, 200) и нажимаем левой кнопкой мыши на пункт
“Добавить линию” (рис. 4.29). Выбираем “Закрыть”, чтобызавершить диалог.

Мультифизические задачи

Задачи, одновременно использующие уравнения из разных областей физики (доменов) или качественно различные модели, принято называть мультифизическими. Связи между доменами могут быть сильными, когда все уравнения аккумулируются в одной общей матрице и решаются совместно, либо слабыми (последовательными), когда задачи в разных доменах решаются последовательно одна за другой. ELCUT использует сильную связь при совместном решении уравнений магнитного поля с уравнениями Кирхгофа для присоединенной электрической цепи (цепно-полевая формулировка), а для большинства остальных мультифизических задач используется последовательная связь (рис. 3).

Рис. 3. Мультифизические связи между отдельными постановками задач

Так, любая задача анализа электрического или магнитного поля порождает электродинамические усилия, которые могут автоматически передаваться в задачу упругости в качестве источника.

Каждая электрическая или магнитная формулировка, рассматривающая ток в проводящей среде, генерирует омические потери, которые могут быть переданы в качестве источника тепла в задачу температурного поля. С другой стороны, электропроводность металлов зависит от температуры, так что результат расчета температурного поля может передаваться в электромагнитный анализ для уточнения удельного сопротивления среды.

Температурное поле также может использоваться задачей анализа упругого напряженного состояния в качестве источника термических деформаций. И, наконец, магнитное состояние нелинейного ферромагнитного материала может запоминаться и экспортироваться в другую магнитную задачу для корректного вычисления дифференциальной индуктивности многообмоточной магнитной системы.

Программа ELCUT

Петербургская компания «Тор» — это компания одного продукта: программы ELCUT . Ключевые слова, характеризующие ELCUT, — инженерное моделирование и квазистатический анализ .

Слово «инженерный» команда ELCUT понимает следующим образом: программа предназначена в том числе и для тех инженеров, которые нуждаются в расчете поля время от времени, и для которых эта задача не обязательно находится в центре профессиональных интересов и навыков. Это означает повышенные требования к простоте и интуитивной ясности использования продукта.

В свою очередь, простота использования означает, что программа не только в полной мере автоматизирует рутинные операции, но и способна предлагать ключевые решения в областях, для которых она является экспертной системой. К примеру, мы полагаем, что модуль решения задачи должен иметь единственную кнопку «решить», не осложняя жизнь пользователю постановкой вопросов о том, какой метод он предпочитает, сколько и каких нужно делать итераций и т. п. Все эти решения разумная программа инженерного анализа должна принять сама, сделав это оптимальным образом.

От пользователя, освобожденного от рутинных операций, ожидается знание физической сути решаемой задачи и детальное понимание сделанных им допущений и упрощений.

История создания ELCUT

Компания основана осенью 1988 г., в основном выходцами из завода «Электросила», где к тому времени функционировала сильная школа численного моделирования электромагнитных полей под руководством профессора В. В. Домбровского.

За более чем 25-летний путь развития программы расширялся диапазон формулировок полевых задач, которые представляют собой подмножество полной системы уравнений Максвелла с упрощениями и допущениями, специально подобранными для решения определенного круга практических задач . К настоящему времени расчет электрического и магнитного поля может проводиться в статическом приближении, в частотной и временной области, с учетом многих видов нелинейности, т. е. зависимости параметров задачи от поля.

ELCUT предоставляет также развитый программный интерфейс , позволяющий писать клиентские приложения в диапазоне от простых скриптов до специализированных систем анализа в предметной области. Ряд сателлитных приложений и утилит с исходными кодами доступен для свободной загрузки с сайта программы.

В последние годы основным направлением развития ELCUT является освоение трехмерного анализа. К настоящему времени (версия 6.3) возможно решение трехмерных статических задач со скалярной потенциальной функцией: электростатика, электрическое поле постоянного тока, температурное поле.

Пользователи ELCUT

Важно иметь в виду, что ELCUT является «коробочным» продуктом, т. е

поставляется пользователям из разных областей инженерной и исследовательской деятельности as is, без кастомизации.

Основной массив пользователей ELCUT в индустрии — предприятия, поставляющие электротехнические изделия и компоненты, такие как электрические машины, трансформаторы , высоковольтные аппараты, кабельная техника , электролитические конденсаторы и др. (рис. 1).

Рис. 1. Области применения ELCUT

Другие пользователи представляют электронное приборостроение, обычно с преобладанием магнитных компонентов (магнетроны, томографы), магнитное обогащение рудных и нерудных материалов . В последние годы усилился интерес строительных проектировщиков к расчету тепловых свойств ограждающих конструкций современных зданий методами численного моделирования температурного поля. Пригодность ELCUT к задачам тепловой защиты зданий подтверждена сертификатом соответствия.

Среди научно-исследовательских организаций пользователями ELCUT являются:

• ведущие научные центры экспериментальной физики;
• создатели электрофизического оборудования;
• ведущие научные центры по электротехнической аппаратуре;
• центры материаловедения, прежде всего в области магнитных материалов;
• организации, занятые оборудованием неразрушающего контроля.

Пользователи отмечают, что ELCUТ является хорошим выбором для первого знакомства с техникой моделирования поля методом конечных элементов. Это способствует распространению ELCUT в ведущих инженерных вузах страны, в основном на кафедрах общей и теоретической электротехники , электрических машин и аппаратов, а также на кафедрах, связанных с сильноточной электронно-лучевой и твердотельной электроникой .

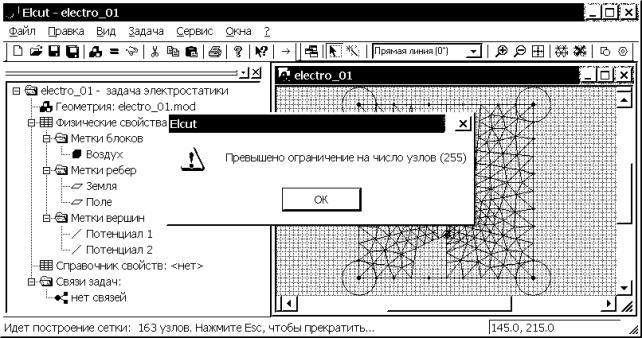
Рис. 4.23. Информационное окно о геометрии выделенных объектов и числе узлов расчетной сетки

7.2. Для повышения точности
расчета количество используемых узлов нужно увеличить, для чего следует
задавать шаг дискретизации вручную. В рассматриваемой задаче можно предположить
существенную неоднородность поля вблизи элементов двухпроводной линии, так что
густота сетки в этих местах должна быть максимальной. Щелкнем левой кнопкой
мыши на одной вершине, затем, удерживая клавишу Ctrl, на второй. Далее отпустив
клавишу Ctrl, нажмем комбинацию клавиш Alt+Enter. В появившемся окне
“Свойства выделенных объектов” изменим в графе “Шаг дискретизации” с
“Автоматический” на “Задан” и введем величину шага дискретизации 4 (см).
Нажимаем “OK”, чтобызавершить диалог.

Расчетная сетка исчезает, а
вокруг каждой из двух вершин возникает дополнительная окружность, которая
позволяет приблизительно оценить шаг дискретизации. Чем больше шаг
дискретизации, тем больше радиус дополнительных окружностей и тем меньше
точность картины поля вблизи этих вершин.

7.3.
Выделим четыре вершины в углах расчетной области и зададим шаг дискретизации
равным 20 (см). Нажимаем кнопку “Построение сетки” на дополнительной панели
инструментов модели. В студенческой версии ELCUT 5.3 появится информационное
окно “Превышено ограничение на число узлов (255)”. Для того чтобы продолжить
работу, нажимаем “OK” (рис. 4.24).

Изменять значение шага дискретизации следует
на границах расчетной области, где картина поля почти однородна. Снова выделяем
четыре вершины в углах расчетной области и задаем шаг дискретизации равным 23
(см). Нажимаем кнопку “Построение сетки” на дополнительной панели
инструментов модели. Расчетная сетка создана. Нажав комбинацию клавиш Alt+Enter,
проверяем число используемых узлов сетки, их 236 (рис. 4.25). Такое количество
узлов вполне приемлемо, теперь возможно решить задачу и посмотреть результаты
решения. Работа с моделью закончена, и её следует сохранить.

Электромагнитная связь проводников

Электрическая и магнитная двумерные модели поля в поперечном сечении могут учитывать не только единственный сигнальный проводник, как в обычных линиях передачи, но и системы из многих проводников

Важно подчеркнуть, что мода колебаний должна быть известна заранее, поскольку для квазистационарных расчетов она входит в число исходных данных: для электрического поля это потенциалы проводников, а для магнитного поля — полный ток каждого проводника

В системе из нескольких проводников параметры линии приобретают матричную форму: матрица частичных емкостей и матрица собственных и взаимных индуктивностей. ELCUT оснащен надстройкой CMatrix для автоматического вычисления матрицы частичных емкостей системы многих проводников (рис. 10).

Рис. 10. Электрическое поле системы нескольких проводников

Надстройка автоматически идентифицирует проводники, входящие в систему (включая линейные и точечные проводники), предоставляет пользователю графический интерфейс для заземления части проводников, определяет необходимое количество полевых задач для решения, автоматически формирует и решает необходимые задачи. Результатом решения каждой задачи, в которой ненулевой потенциал присвоен одному проводнику или паре провод­ников, является полная энергия электрического поля. Сформированная матрица энергии обращается с целью получения матрицы коэффициентов электростатической индукции или эквивалентной ей, но более удобной матрицы собственных и взаимных частичных емкостей.

Аналогичные вычисления могут быть выполнены относительно задачи расчета магнитного поля с целью вычисления матрицы собственных и взаимных частичных индуктивностей.

Параллельные вычисления в LabelMover

Утилита LabelMover предназначена для параметрических расчётов, статистического анализа и оптимизации. Её работа связана с автоматической генерацией и решением большого количества задач ELCUT. Начиная с версии ELCUT 5.8, выполняя параметрический анализ, LabelMover способен решать несколько задач параллельно, используя максимальное число процессорных ядер, имеющихся в вашем компьютере.

Автоматически сгенерированные задачи объединяются в группы для параллельного выполнения. Количество параллельных групп по умолчанию равно количеству процессорных ядер и может быть настроено по усмотрению пользователя.

Подсистемы ELCUT

Последовательность решения задачи в ELCUT предельно проста: нарисовать геометрию модели, сгенерировать расчетную сетку конечных элементов, указать граничные условия, задать свойства материалов, решить дискретную задачу, проанализировать результат решения, извлекая из него локальные и интегральные инженерные параметры.

Перечисленным этапам решения соответствуют подсистемы ELCUT (рис. 4):

• Геометрический редактор для работы с геометрией модели и сеткой конечных элементов. Геометрия может быть прорисована в модели либо импортирована из CAD в формате DXF или SolidWorks. Сетка конечных элементов строится полностью автоматически с гибкими возможностями априорного либо адаптивного управления густотой.
• Подсистема физических данных управляет и хранит сведения о граничных условиях и разнообразных свойствах материалов в разных физических доменах. Некоторые свойства могут нелинейно зависеть от поля либо от температуры. Многие граничные условия могут быть заданы формулой, описывающей их зависимость от координат и времени.
• Редактор электрической цепи используется для решения задач магнитного поля с сопряженной электрической схемой соединения проводников.
• Решатель системы уравнений отличается высокой устойчивостью, отсутствием управляющих параметров и пологой зависимостью времени решения задачи от ее размерности (время пропорционально размерности примерно в степени 1,10…1,15) (рис. 5).
• Подсистема анализа решения (постпроцессор), по отзывам пользователей, является одним из самых разветвленных в индустрии. Он показывает картину поля разными способами (цветная карта, линии поля, семейства векторов, графики, таблицы, анимация), вычисляет локальные и интегральные значения. Интегрирование может выполняться вдоль кривой, по поверхности или по объему.
• Результаты могут быть экспортированы в сторонние программы (Excel, MATLAB, Garfield и др.).

Рис. 4. Подсистемы программы ELCUT

Рис. 5. Зависимость времени решения от размерности задачи

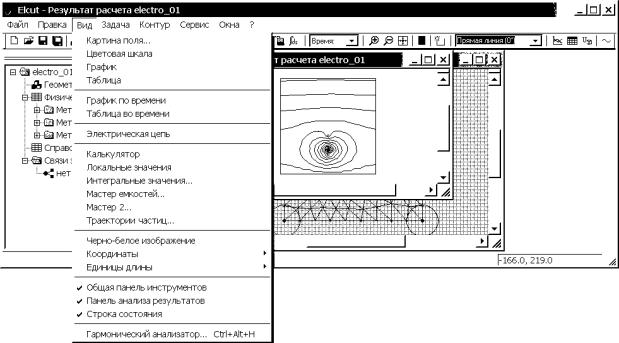
Рис. 4.25. Окончательный вариант расчетной сетки конечных элементов с окном статистики объектов

8. Визуализация
результатов решения

8.1. Для решения задачи щелкаем
левой кнопкой мыши на кнопке “Решить” общей панели инструментов, можно также
воспользоваться командами
“Решить: …” или “Анализ результатов” меню Задача (в последнем случае система
предложит сначала решить задачу, поскольку решение пока отсутствует). Если
после сохранения задачи в ней были произведены какие-либо изменения, ELCUT
предложит сохранить изменения, выбираем “Да”. После утвердительных ответов на
все информационные сообщения системы, когда решение закончится, автоматически
откроется окно результатов решения, в котором будет отражена картина поля (рис.
4.26).

Запоминание магнитного состояния вещества

В большинстве случаев магнитные системы оснащаются ферромагнитными магнитопроводами для концентрации магнитного потока. Ввиду зависимости магнитной проницаемости от поля, расчёт индуктивности нелинейной системы становится сложной задачей, тем более для систем с несколькими катушками и/или постоянными магнитами.

В нелинейной системе рассматривают либо статическую индуктивность, равную отношению потока катушки к току, либо дифференциальную индуктивность, вычисляемую как производная магнитного потока по току.

Как правило, рассчитанные индуктивности используются для моделирования режима реальной или эквивалентной электрической цепи. В этом случае интерес представляют дифференциальные индуктивности и их зависимость от режима работы устройства.

Численный расчёт дифференциальных индуктивностей основывается либо на потокосцеплении с нужным контуром, либо на вычислении полной энергии магнитного поля. В обоих случаях нужно:

1. вывести систему в рабочий режим, задав подходящие значения токов во всех обмотках, и рассчитать картину магнитного поля в рабочем режиме;
2. запомнить магнитное состояние вещества (магнитную проницаемость в каждой точке пространства, занятого ферромагнетиком);
3. решить несколько частных задач, по очереди выключая все токи во всех обмотках, кроме одной.

Начиная с версии 5.8, ELCUT обеспечивает возможность такого расчёта благодаря функции импорта магнитного состояния из другой задачи. Это делается через привычный интерфейс связанных задач.

Задача, импортирующая сохранённое магнитное состояние, становится линейной с математической точки зрения, сохраняя, тем не менее, реальные свойства вещества в окрестности рабочей точки. Тем самым, вычисление дифференциальных индуктивностей становится весьма простым делом, в том числе и для многообмоточных систем.

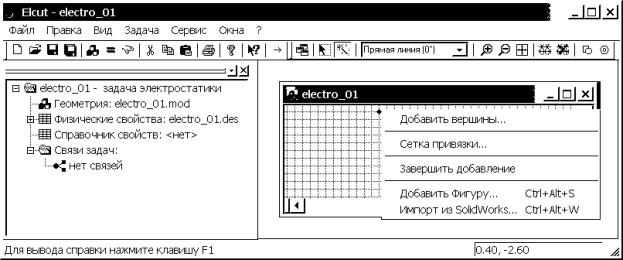
Рис. 4.7. Интерфейс новой задачи ELCUT с окном геометрической модели

3. Создание
геометрических элементов

3.1. При работе в окне
геометрической модели можно находиться в двух основных режимах: режиме выделения объектов (курсор мыши
в виде стрелочки), режиме вставки
вершин/ребер (курсор мыши в виде перекрестия при этом красной точкой выделяется
ближайший узел сетки привязки). В режиме вставки рисуются объекты
геометрической модели, при этом для выбора типа контура ребер следует
пользоваться соответствующей вкладкой на дополнительной панели инструментов модели
(см. рис. 3.7).

Наиболее удобно переходить
из одного режима в другой по клавише Insert или щелкнув левой кнопкой
мыши на соответствующей кнопке или дополнительной панели инструментов модели.
Можно также использовать команду “Режим вставки” из меню Правка.

3.2. Определимся с границами
расчетной области. Особых требований по условиям задачи нет, поэтому следует
исходить из физических особенностей задачи. Расчетная область может быть
представлена любой геометрической фигурой: квадратом, прямоугольником или
окружностью (в зависимости от геометрии задачи). Вполне достаточно, чтобы
границы расчётной области имели линейные размеры, превышающие размеры
исследуемого поля в 3-5 раз. Так как по условию задачи раздела 1.6 расстояние
между электродами составляет 0,8 м, расчетную область выбираем квадратом с
ребром 200 см и границами (-100 см £ х £ 100 см, 0 £y£ 200 см). В дальнейшем все
координаты в сантиметрах.

3.3. На примере
рассматриваемой задачи покажем, как создавать расчетную область по вершинам в ELCUT. Чтобы
создать одиночную вершину вручную, следует в режиме вставки перевести курсор
мыши в узел сетки с требуемой координатой и сделать двойной щелчок левой
кнопкой мыши – в месте узла автоматически создастся вершина. Вводить вершины
можно вручную при создании ребер, при этом необходимо переводить курсор мыши в
нужные точки. В большинстве случаев для ввода вершин удобнее применять
соответствующее меню “Добавление вершин”.

Введем четыре вершины
расчетной области и соединим их ребрами. Перейдем в режим вставки нажатием
клавиши Insert. Нажимаем правую кнопку мыши и в возникшем
контекстном меню (см. рис. 3.12) выбираем левой кнопкой мыши команду “Добавить
вершины” (рис. 4.8). Появляется окно “Добавление вершин” (см. рис. 3.11).

Выводы

ELCUT на сегодня является зрелым «коробочным» продуктом, пригодным для использования в разных отраслях инженерной, исследовательской и академической деятельности .

Для задач электроники, в частности двумерного расчета поля линий передачи в поперечном сечении, прямо «из коробки» ELCUT способен:

• вычислять волновое сопротивление линий передачи с неограниченным разно­образием формы, размеров и расположения провод­ников и диэлектриков, при условии, что заранее известна мода колебаний;
• вычислять потери в диэлектрике и в проводниках с учетом скин-эффекта и поверхностного эффекта;
• вычислять индуктивность проводников на переменном токе;
• вычислять матрицы частичных емкостей и частичных индуктивностей системы из нескольких проводников;
• оценивать тепловое состояние элементов в 2D- и 3D-моделях при задании условий конвективного теплообмена;
• проводить оптимизационный и статистический анализ.

Помимо развитого графического интерфейса, ELCUT предоставляет опытным пользователям и разработчикам програм­мный интерфейс для широкого круга задач автоматизации: от написания простых скриптов для выполнения рутинных операций до интеграции ELCUT в существующий многопрограм­мный поток проектирования радиоэлектронной аппаратуры.

Программный интерфейс, называемый ActiveField, выполнен по технологии COM/ActiveX. Он содержит сотни объектов, методов и свойств, которыми можно пользоваться из большинства современных языков программирования на платформе Windows в одномашинной и многомашинной конфигурациях, а также из прикладных пакетов (MS Office, MATLAB и пр.).

На сайте программы представлены в свободном доступе пользовательская документация, а также обширный набор инструкций, видеоматериалов, записанных семинаров и технических статей по применению ELCUT в различных отраслях индустрии.